As you observed in the introduction, rational functions typically have asymptotes, and sometimes have holes.
Vertical asymptotes, horizontal asymptotes, and holes in the graph cause some of the variation in the graph. In the applet below, you will explore how varying the parameters in a rational function can affect the asymptotic behavior of the graph of the function.
In this section, you will investigate rational functions of the following form:
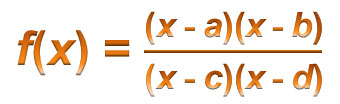
Rational functions of this form are ratios of two quadratic expressions, so the degree of the numerator and the degree of the denominator are both equal to 2. The quadratic expressions are presented in factored form to make it easier to identify patterns.
![]() Click on the image to access the applet. Use the sliders to change the values of a, b, c, and d in the applet. Use the applet to complete the table below. Use the data in the table to answer the conclusion questions that follow.
Click on the image to access the applet. Use the sliders to change the values of a, b, c, and d in the applet. Use the applet to complete the table below. Use the data in the table to answer the conclusion questions that follow.
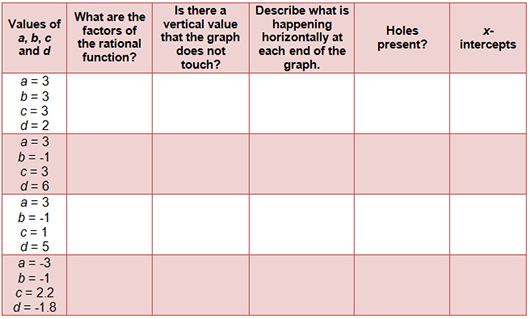



As you worked through this section, the applet provided you with a chance to see several types of discontinuity in the graph of a rational function. What are two types of discontinuity in which the graph is undefined?

Finding x-intercepts is something that you have done in previous lessons. Without looking at the graph of a rational function, how can you find the x-intercepts?
