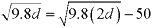In this section real life problems provide practice solving equations with square roots.
- The period of the pendulum (T) is the time it takes the pendulum in seconds to move back and forth once as shown in the equation:
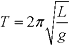
where L is the length in meters and g is the acceleration due to gravity (approximately 9.8 m/sec2.)
Answer the questions below.

Source: Flickr
- In 1851, French physicist Léon Foucault hung a 67 m pendulum from the dome of the Panthéon in Paris. Foucault's pendulum was the first simple proof that the Earth rotated in an easy-to-see experiment. What was the period of Foucault’s pendulum?
- If Foucault had done his experiment on the moon where gravity is 1/6th that of Earth’s, what would have been the period of his pendulum?
- If Foucault had wanted the period of his pendulum to be 10 seconds, what length would he have needed to make his pendulum? (Assume he’s still on Earth.)
- If Foucault has a new pendulum of length x, it would have a period of 2π
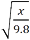 . If he then halves the length, the new period is 5 seconds shorter. What was the original length, x, of the pendulum?
. If he then halves the length, the new period is 5 seconds shorter. What was the original length, x, of the pendulum?
 Watch the video if you need to see a solution to this problem.
Watch the video if you need to see a solution to this problem.
- Explain in your own words how you would solve the following equation for d using graphs on your graphing calculator.
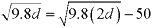
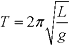
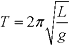

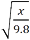 . If he then halves the length, the new period is 5 seconds shorter. What was the original length, x, of the pendulum?
. If he then halves the length, the new period is 5 seconds shorter. What was the original length, x, of the pendulum?
![]() Watch the video if you need to see a solution to this problem.
Watch the video if you need to see a solution to this problem.