This section uses real world problems to formulate square root equations.
Square roots are used in a variety of real-world applications as shown below.
To review the square root function, refer to Algebra 2, module 6, lesson 2.
Example 1: The velocity v (in feet per second) of a jet can be approximated by the equation:
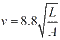
Where A is the area of the wings (in square feet) and L is the lift (in Newtons).
Interactive pop-up activity. Assistance may be required.
Answer the questions below. Check your answer by clicking on the "Check Your Answer."
- How many independent variables are there in this formula?
- What are the independent variables, and what do they represent in the problem situation?
- What is the dependent variable, and what does it stand for in the problem?
- If a Boeing 747 jet has a wing area of 5825 square feet and they produce a lift of 2,834,400 Newtons, what is the equation for the velocity?
- If the velocity of an airplane is 200 ft/sec and its wing area was 4000 sq. feet, what equation would you write to find the lift of the wings?
Example 2:
The period of time it takes a pendulum to make one complete back and forth movement with respect to its length and gravity is an example of a square root equation.

 Please click on the link and follow the directions. Pendulum
Please click on the link and follow the directions. Pendulum
Answer the questions below. Check your answer by clicking on the "Check Your Answer".
- Drag the pendulum to make the angle around 80° and the length approximately 5 m.
- Press the PLAY button and then press the PAUSE button when the pendulum completes one period and is back to 80°. About how long did it take?
- Now press the RESET button.
- Keep the pendulum at an angle around 80°, but shorten the pendulum to 2 m.
- Press the PLAY button and then press the PAUSE button when the pendulum completes one period and is back to 80°. About how long did it take this time?
- What conjecture would you make regarding the length of a pendulum and its period?
For a pendulum, the period (T) in seconds can be found by 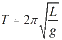 where L is the length in meters and g is the acceleration due to gravity (g≈9.8 m/sec2.)
where L is the length in meters and g is the acceleration due to gravity (g≈9.8 m/sec2.)

Source: Foucault's Pendulum, David Van Bael, Flickr
- In 1851, French physicist Léon Foucault hung a 67 m pendulum from the dome of the Panthéon in Paris. Foucault's pendulum was the first simple proof that the Earth rotated in an easy-to-see experiment. What is the equation for the period of Foucault's pendulum?
- If Foucault had done his experiment on the moon where gravity is 1/6th that of Earth's, what equation would you write to find the new period?
- If Foucault had wanted the period of his pendulum to be 10 seconds, what equation would he use to find the necessary length? (Assume he's still on Earth.)
- If Foucault has a new pendulum of length x, it would have a period of
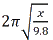 . If the length is halved, the new period is 5 seconds shorter. Write an equation that could be used to find the original length, x.
. If the length is halved, the new period is 5 seconds shorter. Write an equation that could be used to find the original length, x.
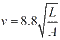
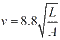
 Source: 2 Jumbo Jets Flying in Parallel, alisatwell, alisatwell.com
Source: 2 Jumbo Jets Flying in Parallel, alisatwell, alisatwell.com
![]() Please click on the link and follow the directions. Pendulum
Please click on the link and follow the directions. Pendulum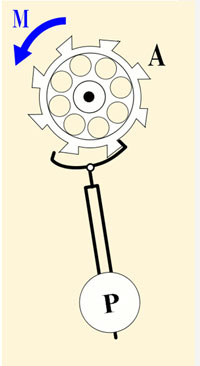 Source: Clock-pendulum, ЮК, Wikimedia Commons
Source: Clock-pendulum, ЮК, Wikimedia Commons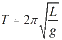 where L is the length in meters and g is the acceleration due to gravity (g≈9.8 m/sec2.)
where L is the length in meters and g is the acceleration due to gravity (g≈9.8 m/sec2.)
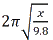 . If the length is halved, the new period is 5 seconds shorter. Write an equation that could be used to find the original length, x.
. If the length is halved, the new period is 5 seconds shorter. Write an equation that could be used to find the original length, x.