In this section, you will solve square root inequalities containing a numerical value instead of y.
You must compare both sides of the inequality.
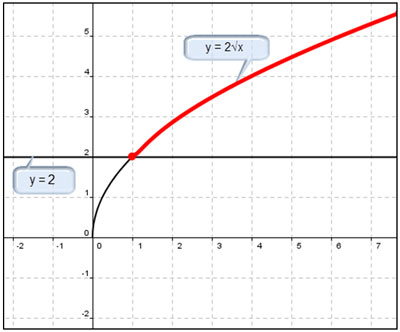
Example: Solve 2√x ≤ 2 and 2√x ≥ 2
Step 1: Both ≤ and ≥ are solid lines.
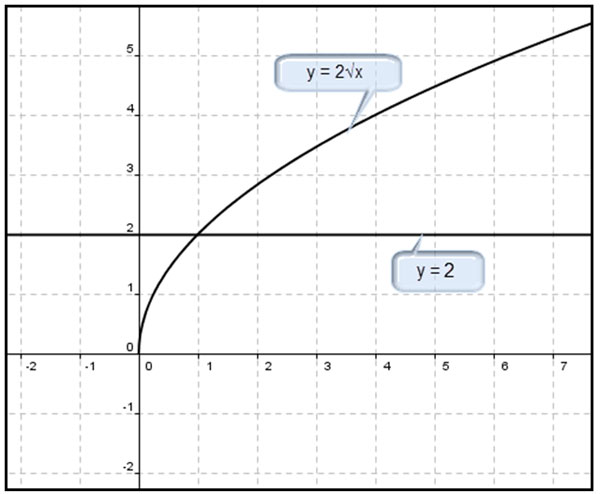
Step 2: Graph both sides of the inequality as functions on the same coordinate plane.
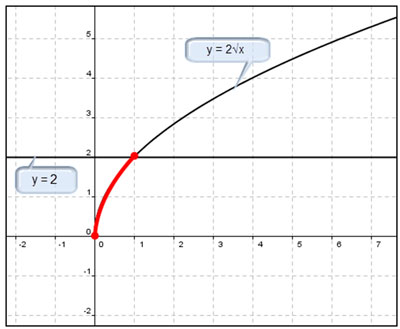
Graph y = 2√x and y = 2.

Step 3: Find where the function y = √2x is greater than y = 2 and less than y = 2.
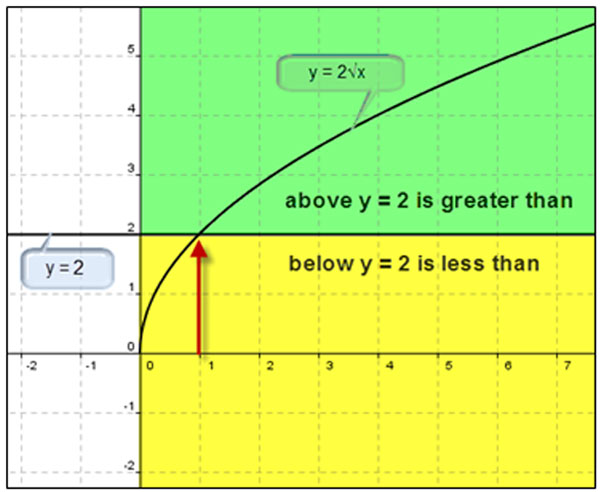
Going back to our original example: √x ≤ 2 and √2 ≥ 2
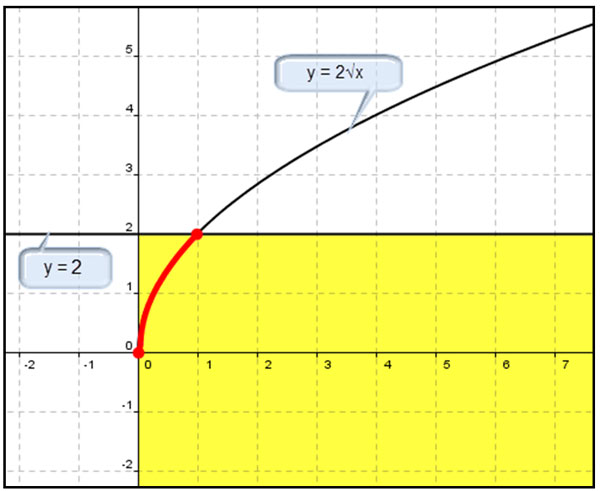
If you are graphing √2x ≤ 2, then you want the less than part which is below
y = 2, the yellow area.
Because the original inequality only contained an x-variable, then the solution only has x’s.
The solution to the graph of √2x ≤ 2 is 0 ≤ x ≤ 1.
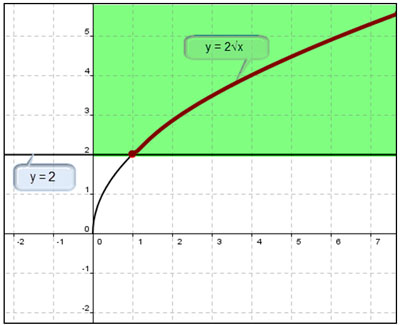
If you are graphing √2x ≥ 2, then you want the greater than part which is above y = 2, the green area.
The solution to the graph of √2x ≥ 2 is x ≥ 1.