Wooden Roller Coaster, Wikimedia

Six Flags Fiesta Texas has many exciting roller coasters. Have you ever wondered how fast you were going at the bottom of one of those steep drops? The relationship between a roller coaster’s velocity (in feet per second) at the bottom of a drop and the height (in feet) of that drop can be modeled by the square root function V = 8 √h.

Square root functions can be represented in multiple ways. In this lesson, you will learn how to generate different representations of the same function. The representations can be algebraic, tabular, graphical, or verbal.

Algebraic Representation

An algebraic representation is an expression, equation, or function. In the roller coaster example, V represents velocity in feet per second, and h represents the height in feet.

Tabular Representation

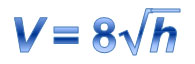
To represent this function in a table, choose four or five values to substitute for h, and then solve to find the values of the velocity, V. You can use the table function in your graphing calculator to obtain the values, or you can go to the following GTable applet by clinking on the image below.

Interactive popup. Assistance may be required.

Need additional directions?

Interactive popup. Assistance may be required. Click here for a sample of table values for this function.

h	Process	V
0	8√0	0
1	8√1	8
9	8√9	24
64	8√64	64
121	8√121	88
169	8√169	104

Verbal Representation

To represent this function verbally, you can say that the velocity of the roller coaster at the bottom of a drop equals 8 times the square root of the height of the roller coaster at the point of the drop. Another way to say this is the height of the roller coaster at the point of a drop is equal to the square of the velocity at the bottom of the drop divided by 8.

Graphical Representation

To represent this graphically, you can use the h and V values from the table to plot these points on a coordinate grid. Connecting the points gives you a graphical representation.

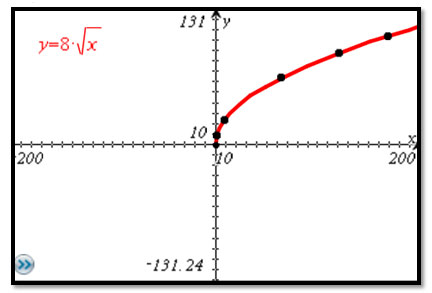
The Superman ride at Six Flags over Texas has a 169-foot drop. In feet per second, how fast are you going when you reach the bottom? Use one of the representations above to find the answer.

Interactive popup. Assistance may be required.

Check Your Answer

104 ft/sec