In this resource, you will learn how to determine the solution(s) of a quadratic equation using tables.
When a quadratic equation is solved, we are actually finding the x-intercepts. Since the y-coordinate of the x-intercept is 0, we must first set the quadratic equation equal to 0.
y = ax2 + bx + c, where a ≠ 0
or
0 = ax2 + bx + c, where a ≠ 0
This is called standard form.
Understanding the parts of an equation:
What do you know about x in the equation below?
0 = 2x2 − 6x − 36

What does the equal sign tell us about the equation?
Interactive popup. Assistance may be required.
The equal sign tells us that the expressions on either side have the same value. Therefore for the given equation, we are looking for an x-value that will make the value of the expression 2x2 − 6x − 36 the same as 0.

A table on the calculator shows how the value of the expression changes as the value of x changes.
| Step 1: Enter the expression into [Y=1]. | 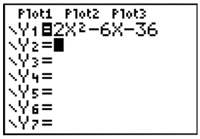 |
| Step 2: Go to the table. | |
| Step 3: Use the up and down arrows to scroll up and down the table. | 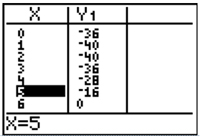 |
Remember that the x column represents the value of x and the y1 column represents the value of the expression 2x2 − 6x − 36.
What is the value of 2x2 − 6x − 36 when x is 1?
Interactive popup. Assistance may be required.
-40

What is the value of 2x2 − 6x − 36 when x is -5?
Interactive popup. Assistance may be required.
44

What is the value of 2x2 − 6x − 36 when x is 10?
Interactive popup. Assistance may be required.
104

As you scroll up and down the table, what is happening to the values in y1?
Interactive popup. Assistance may be required.
The values in the y1 column increase when x is less than -3. The values decrease when x is between -3 and 1. Finally, the values increase again when x is greater than 2.

Since we are solving for x in the equation, 0 = 2x2 − 6x − 36
, find the x-values for which y1 has a value of 0.
Interactive popup. Assistance may be required.
The x values that make y1 = 0 are x = 6 or x = -3. These are the solutions to the equation. 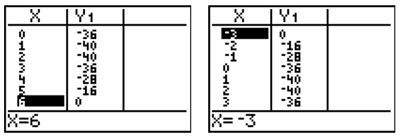

Further examination of the x-intercepts connection to the solution:
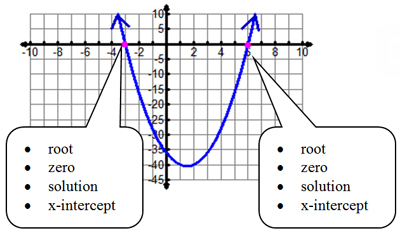
What do you remember about x-intercepts?Interactive popup. Assistance may be required.
You should recall that an x-intercept(s) is where the graph crosses the x-axis, this is also called the roots or the zeros since the y-value is zero at these points or y = 0.

Explain why the x-intercept is also called a solution.Interactive popup. Assistance may be required.
To solve a quadratic equation, find the x-value(s) that make the quadratic equation equal to 0. The solution(s) is a point(s) on the graph where x is the solution and 0 is the y-value, this point(s), (x, 0), is the x-intercept(s).

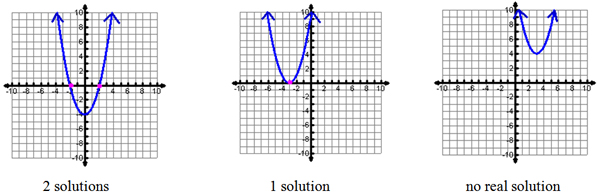
Below are graphs showing the possible number of solutions or x-intercepts for quadratic equations.