
In some cases, you will encounter quadratic inequalities that may not have a solution set, while other inequalities may have an infinite number of solutions. This means that it is possible that either no number would satisfy the inequality or every real number would satisfy the inequality.
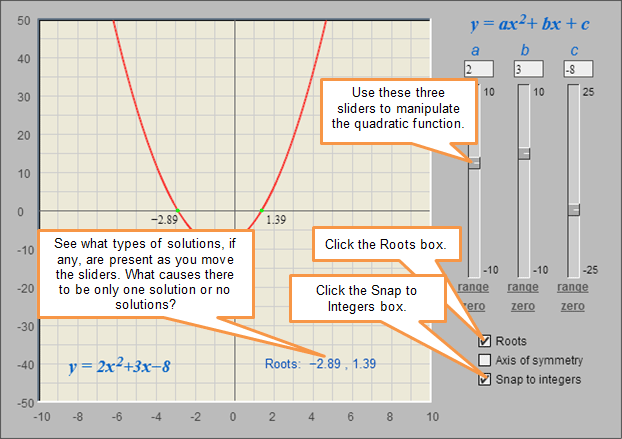
Think back to your experience with quadratic functions. What would cause a quadratic equation to have no solution? What would cause a quadratic equation to have only one solution? How would this information apply to quadratic inequalities? The applet below will help you answer these questions.

![]() Click on the image to access the applet. Using this applet, check the box to show the "Roots" and the box for "Snap to Integers." This will keep your sliders as integer values. As you move the sliders for b and c, see how the roots change and if solutions are present. At some point, set the values for b and c equal to zero, and then adjust the slider for a.
Click on the image to access the applet. Using this applet, check the box to show the "Roots" and the box for "Snap to Integers." This will keep your sliders as integer values. As you move the sliders for b and c, see how the roots change and if solutions are present. At some point, set the values for b and c equal to zero, and then adjust the slider for a.

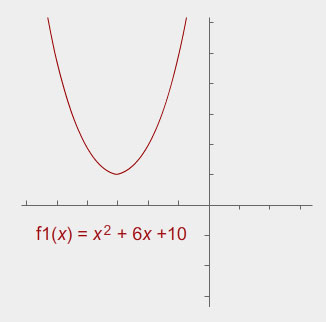
If the quadratic function does not have roots, there may or may not be an interval of values that satisfy the inequality. Depending on the inequality sign, it may not have a solution set, or the solution set may be all real numbers.



Additionally, you may encounter compound quadratic inequalities, especially when you are working within a particular context or problem situation. For example, in April 2013, Austin, Texas, was the host city for the MotoGP event 2013 Circuit of the Americas. To begin the weekend, Miles Dashier and Jeff Provenzano performed a based jump from the 251-foot tall Tower of the Americas.
Not only were the jumpers wearing cameras to film the jump, several local and national journalists were on the ground with still cameras snapping pictures during the jump. In order to get the best perspective of the jump with a still picture camera, the journalists had to capture the images between 151 and 215 feet above the ground. If the entire fall took less than four seconds, during what interval of time did the journalists have to snap their still images?
Note that any object influenced by gravity falls freely according to the equation h(t) = −16t2 + vot + ho, where vo is the initial velocity, ho is the initial height in feet above the ground, and t represents time measured in seconds.
To set up the problem, first substitute the information from the problem into the function.

 Interactive popup. Assistance may be required.
Interactive popup. Assistance may be required.
151 < -16t2 + 251 < 215 -100 < -16t2 < -36 |
Using inverse operations, subtract 251 from each side of the inequality to begin isolating the variable. |
-100 over -16 -100 -16 > -16 t squared over -16 -16t2 -16 > -36 t squared over -16 -36 -16 6.25 > t2 > 2.25 |
Next, divide each section of the inequality by −16. Remember the rules about multiply and dividing inequalities by a negative number! |
|
√6.25 > √t2 > √2.25 |
To continue isolating the variable, take the square root of each section. Since time is normally considered to be positive, you can ignore the negative square roots for this problem. |
|
2.5 > t > 1.5 |
This will leave you with the compound inequality that t is less than 2.5 and greater than 1.5, which means the journalists will have to take their images between 1.5 and 2.5 seconds after the jumpers leave the platform. |

What does it mean for a quadratic inequality to have no solution?

In working with compound quadratic inequalities, is it possible to use the quadratic formula?
Interactive popup. Assistance may be required.
Remember that to find area of a rectangle, you have to multiply the length and the width. Let x be the width of the rectangle. Interactive popup. Assistance may be required.
Interactive popup. Assistance may be required.
x(x + 8) > 240 |
Using inverse operations, collect all of the terms of the quadratic inequality on one side. In this case, you must also distribute the x. |
x2 + 8x − 240 > 0 |
To help guide your thinking, change the inequality sign to an equal sign. |
|
x2 + 8x − 240 = 0 |
One way to solve this related quadratic equation is to use factoring. The factors of −240 that sum to +8 are +20 and −12. |
x = -20 and x = 12 |
The roots for this quadratic inequality are at -20 and positive twelve. |
| Interval (-∞ ,-20) | Interval (-20,12) | Interval (12,∞) |
| Inequality x < -20 | Inequality -20 < x < 12 | Inequality x > 12 |
| Example test point: 22 | Example test point: 0 | Example test point: 14 |
x(x + 8) > 240 |
x(x + 8) > 240 |
x(x + 8) > 240 |
| True. However, since we do not measure distances with negative numbers, the width can not be less than -20. In this context, this interval will not satisfy the inequality. | False | True |
The solution to x(x + 8) > 240 is x > 12 .
For the rectangle to have an area that is greater than 240 square inches, the width must be greater than 12 inches. This also means that the length will be 8 inches more than the width, so the length must be greater than 20 inches.

Interactive popup. Assistance may be required.
Select the best method possible to find the solution to the inequality. If you are having trouble finding factors, use the quadratic formula. Interactive popup. Assistance may be required.
Interactive popup. Assistance may be required.
|
2x2 − 2x > -5 |
Use inverse operations to collect all of the terms of the quadratic inequality on one side of the inequality. |
|
2x2 − 2x + 5 > 0 |
To help guide your thinking, change the inequality sign to an equal sign. |
|
a = 2, b = -2, c = 5 |
To use the quadratic formula, determine the values for a, b, and c, which are the coefficients of the quadratic equation. |
|
x = negative b plus or minus the square root of b squared minus four a c over 2a -b ± √b2 − 4ac 2a |
State the quadratic formula. |
x = -(-2) plus or minus the square root of negative 2 squared minus 4(2)(5) over 2(2) -(-2) ± √(-2)2 − 4(2)(5) 2(2) |
Substitute the value of a, b, and c in the appropriate locations in the formula. |
|
x = 2 plus or minus the square root of 4 minus 40 over over 4 2 ± √4 − 40 4 |
Simplify the expression beneath the radical. |
|
x = 2 plus or minus the square root of negative 36 over 4 2 ± √ -36 4 |
Since the radicand is negative, there are no real roots for the quadratic equation. |
Since there are no real roots for the related equation, there are no intervals to test. This suggests that there are either no real solutions to the inequality or that all real values of x will make the inequality true. To determine which case is true for this inequality, look at the graphs of the left member and right member of the related equation, as you did in the conclusion questions.
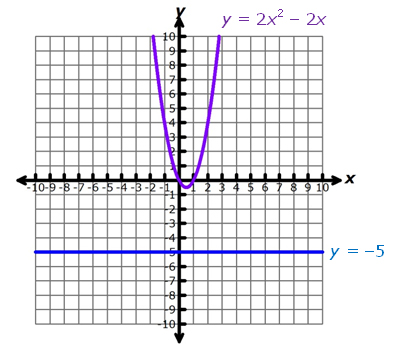
From the graph, you can see that all values of 2x2 – 2x are greater than −5. Use this observation to test a few points in the original inequality.
Example test point: −1 |
Example test point: 0 |
Example test point: 3 |
2(−1)2 – 2(−1) > −5 |
2(0)2 – 2(0) > −5 |
2(3)2 – 2(3) > −5 |
2(1) + 2 > −5 |
2(0) + 0 > −5 |
2(9) + 6 > −5 |
2 + 2 > −5 |
0 + 0 > −5 |
18 + 6 > −5 |
4 > −5 |
0 > −5 |
24 > −5 |
True |
True |
True |
The inequality 2x2 – 2x > −5 is true for all real values of x.

Interactive popup. Assistance may be required.
If you are having trouble factoring, try the quadratic formula. Interactive popup. Assistance may be required.
Interactive popup. Assistance may be required.
|
3x2 < 6x + 5 |
Use inverse operations to collect all of the terms of the quadratic inequality on one side of the inequality. |
|
3x2 − 6x − 5 < 0 |
To help guide your thinking, change the inequality sign to an equal sign. |
a = 3, b = −6, and c = −5 |
To use the quadratic formula, determine the values for a, b, and c, which are the coefficients of the quadratic equation. |
|
x = negative b plus or minus the square root of b squared minus four a c over 2a -b ± √b2 − 4ac 2a |
State the quadratic formula. |
|
x = -(-6)plus or minus the square root of (-6) squared -4(3)(-5) over 2(3) -(-6) ± √-62 − 4(3)(-5) 2(3) |
Substitute the value of a, b, and c in the appropriate locations in the formula. |
|
x =
6 plus or minus the square root of 36 + 60 over 6
6 ± √36 + 60
6
|
Simplify the expression beneath the radical. |
|
x =
6 plus or minus four times the square root of 6 over 6
6 ± 4 √6
6
|
If perfect squares are present, factor out the appropriate root. Reduce the values of the root to simplest terms. |
|
x =
3 plus 2 times the square root of 6 over 3
3 + 2 √6
3
and
x =
3 minus 2 times the square root of 6 over 3
3 - 2 √6
3
|
These roots are where the graph of the quadratic inequality would cross the x-axis. |
| Interval (-∞, 3 minus 2 times the square root of 6 over 3 3 - 2 √6 3 ) | Interval ( 3 minus 2 times the square root of 6 over 3 3 − 2 √6 3 , 3 plus 2 times the square root of 6 over 3 3 + 2 √6 3 ) | Interval ( 3 plus 2 times the square root of 6 over 3 3 + 2 √6 3 , ∞) |
| Inequality x < 3 minus 2 times the square root of 6 over 3 3 − 2 √6 3 | Inequality 3 minus 2 times the square root of 6 over 3 3 − 2 √6 3 < x < 3 plus 2 times the square root of 6 over 3 3 + 2 √6 3 | Inequality x > (3 + 2 √(6 ))/3 |
| Example test point: -1 | Example test point: 0 | Example test point: 3 |
3x2 < 6x + 5 |
3x2 < 6x + 5 |
3x2 < 6x + 5 |
| False | True | False |
The solution to 3x2 < 6x + 5 is 3 minus 2 times the square root of 6 over 3 3 - 2 √6 3 < x < 3 plus 2 times the square root of 6 over 3 3 + 2 √6 3 .
