In this section, you will create a graph from a quadratic equation.

Before graphing a parabola, there are three things you need to do:

  1. Identify the vertex of a parabola.
  2. Identify the axis of symmetry.
  3. Use symmetry to find two sets of matching points across the axis of symmetry.

If the equation is in vertex form, y = a (x – h)2 + k where a ≠ 0, then (h, k) is the vertex.

Also, the axis of symmetry must pass through the vertex point of (h, k) and it is a vertical line, which means the equation for the axis of symmetry is x = (x-coordinate of the vertex) h.

Example

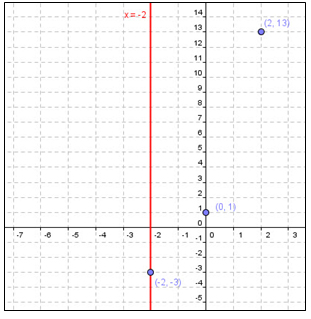
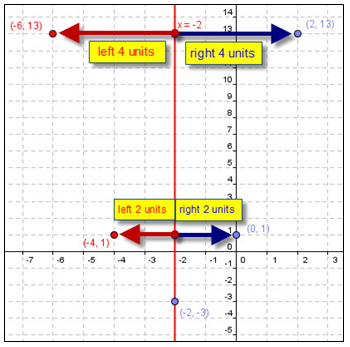
Graph y = (x + 2)2 – 3

Step 1: Find the vertex using the vertex formula: y = a (x – h)2 + k

The vertex is at (- 2, - 3) since the equation is in vertex form → h = - 2 and k = - 3.

Step 2: Find the axis of symmetry.

The axis of symmetry is the vertical line that passes through the vertex and its equation is x = - 2.

Step 3: Pick two values for x and substitute them into the equation to find their y-coordinates.

Let’s pick x = 0 and x = 2. (You may choose any number for x, but it is usually easier to work with integers.)

Substitute: x = 0 → y = (0 + 2)2 – 3 → so y = 1 → (0, 1)

Substitute: x = 2 → y = (2 + 2)2 – 3 → so y = 13 → (0, 13)

Step 4: Plot the three points and draw in the axis of symmetry.

Step 5: Reflect the points across the axis of symmetry to find two more points.

Another Example

Extra Practice

Example

Graph y = 2x2 – 8x + 3

When a quadratic equation is written in standard form, you will still follow the same steps.

Step 1: Find the Vertex—The vertex isn’t obvious when a quadratic equation is written in standard form.

  1. To find the x-coordinate of the vertex, use the formula x = − b over 2a b 2a where a and b are the coefficients of x2 and x respectively; therefore, y = 2x2 – 8x + 3 → a = 2 and b = - 8

    x = − b over 2a b 2a = − x = − negative eight over two times two (-8) 2(2) = − x = − negative eight over four (-8) 4 = −(-2) = 2
    (Note: this is also the axis of symmetry.)

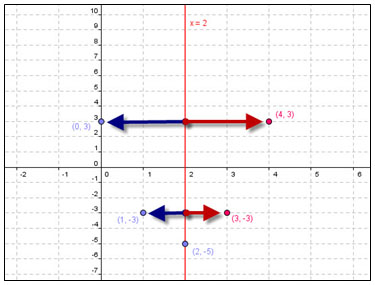
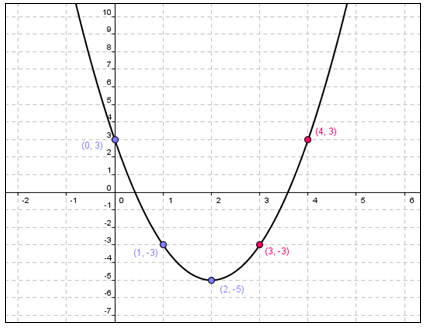
  2. Substitute the x- coordinate into the equation to find the y-coordinate for the vertex.

    3. y = 2x2 – 8x + 3
    y = 2(2)2 – 8(2) + 3
    y = 8 – 16 + 3
    y = - 5

  3. The vertex of the parabola is at (2, - 5).
Step 2: Find the axis of symmetry.
  1. The formula x = − b over 2a b 2a also gives you the equation of the axis of symmetry or you can use your vertex, x = 2.
Step 3: Pick any two values for x (that are not x = 2 from the vertex) and substitute them into the equation to find their y-coordinates.

Let’s pick x = 0 and x = 1.

Substitute x = 0 → y = 2(0)2 – 8(0) + 3 → so y = 3 → (0, 3)

Substitute x = 1 → y = 2(1)2 – 8(1) + 3 → so y = - 3 → (0, - 3)

Step 4: Plot the three point, draw in the axis of symmetry, then reflect the points across the axis of symmetry.

Step 5: Sketch your parabola.

Extra Practice