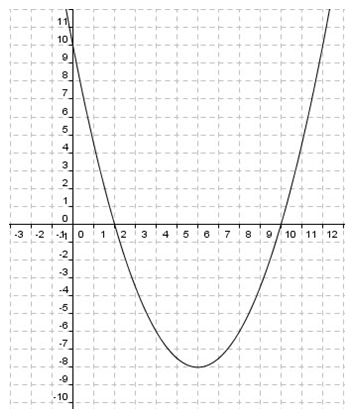
Verbal Description of the Quadratic Function

• The graph has x-intercepts at (2,0) and (10,0).
• The parabola has zeros at x = 2 and 10.
  The graph crosses the x-axis at x=2 and 10.
• The function has 2 real rational roots.
  The parabola crosses the x-axis twice and
  2 and 10 are rational numbers.
• The graph has a y-intercept at (0, 10).
• The vertex of the parabola is at (6, -8).
  This is the lowest point on the graph and it is also where the graph changes direction.
• The parabola opens up so it has a minimum.
  This is the lowest point on the graph. The minimum is at the vertex.
• The axis of symmetry is x = 6.
  This is the vertical line that passes through the vertex and divides the parabola into 2 symmetric halves.
• The parabola decreases when x < 6 and increases when x > 6.
  From left to right, the y-coordinates are getting smaller so the graph is going down until it gets to the vertex point, where it changes direction and begins to go up.