In this section you will be translating a graph into a verbal description.
A verbal description of a quadratic function using its graph mentions the following:
- the location of any zeros, roots, or x-intercepts
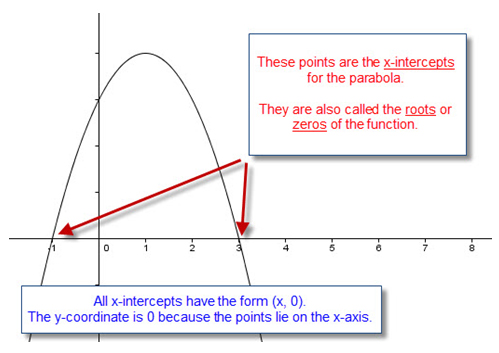
- the type of zeros, roots, or x-intercepts
Possible roots include: real, rational, irrational or imaginary numbers. Remember you must actually know the numerical value to be able to decide whether that number is rational or irrational.
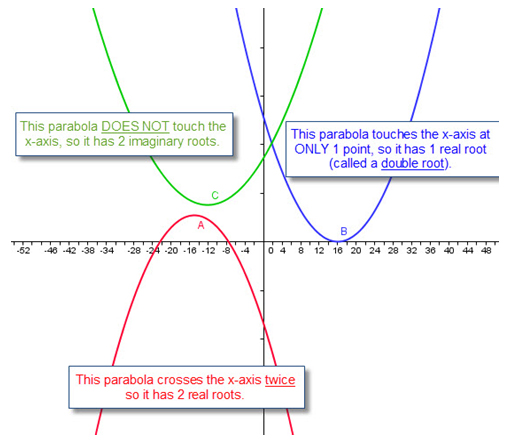
Study the graphs below to determine from a graph whether a parabola has real or imaginary roots.
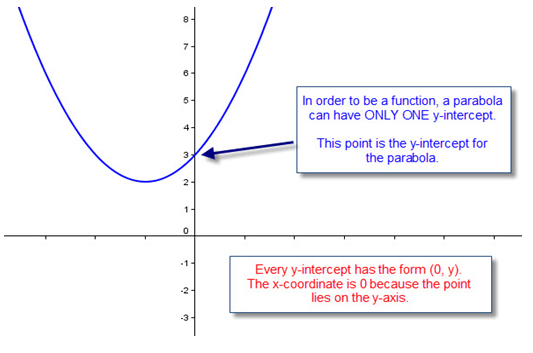
- the location of the y-intercept
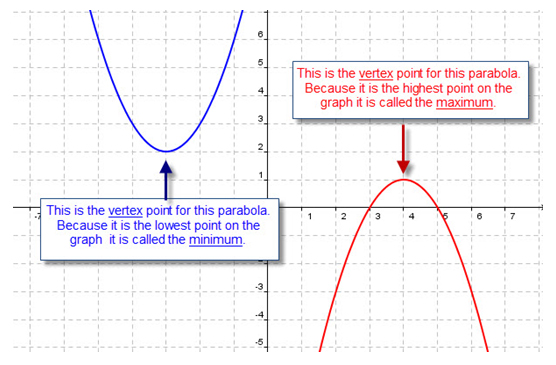
- the location of the vertex
- whether the parabola has a minimum or maximum
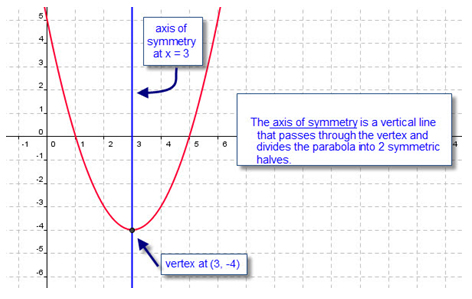
- the location of the axis of symmetry
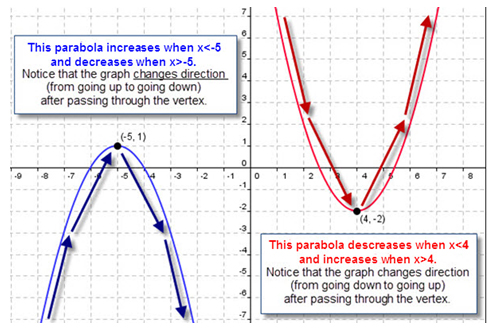
- where the parabola is increasing or decreasing
To review:
When writing a verbal description for a quadratic function using its graph, identify its critical attributes and behavior which include:
- the location of any zeros, roots, or x-intercepts,
- the type of zeros, roots, or x-intercepts,
- the location of the y-intercept,
- the location of the vertex,
- whether the parabola has a minimum or maximum
- the location of the axis of symmetry
- whether the parabola opens up or down
- where the parabola is increasing or decreasing







