Untitled Document

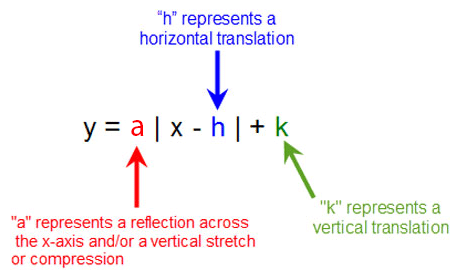
In this section, all the transformations will be presented together.

It is important to be able to identify how each parameter in the vertex form equation affects the graph.

y = a|x-h| + k, where a represents a reflection across the x-axis and/or a vertical stretch or compression, k represents a vertical translation, and h represents a horizontal translation

Example

How is the graph f(x) = 2 | x + 3 | - 1 translated from the parent function y = | x |?

a = 2 is a reflection across the x-axis, a stretch creating a narrow graph
h = -3 is a horizontal translation, moving the graph to the left three units
k = -1 is a vertical translation, moving the graph down one unit

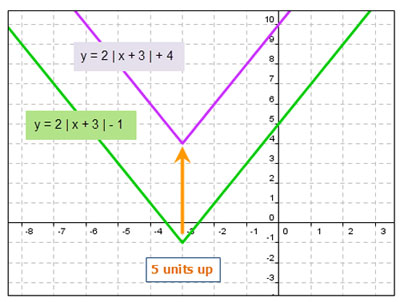
If the graph of f(x) = 2 | x + 3 | - 1 is translated 5 units up, what is the new equation?

A translation of 5 units up is vertical and affects ONLY the “k” in the equation.

If f(x) = 2 | x + 3 | - 1 ⇒ k = -1.

To translate this graph up, you should add to “k”.

Starting at -1 and moving up 5 units, gives you -1 + 5 = 4, so the new h = 4.

The new equation is: f(x) = 2 | x + 3 | + 4

The new graph is:

graphing calculator screen showing f(x) = 2 | x+3 |+4 and f(x) = 2 | x+3 |-1

The tables of values for the two equations are:

f(x) = 2 | x + 3 | − 1

x	y
0	5
-1	3
-3	-1
-5	3
-6	5

and

**Vertex

f(x) = 2 | x + 3 | + 4

x	y
0	10
-1	8
-3	4
-5	8
-6	10

**Vertex