In the previous section, you used a generic function to examine patterns in the horizontal and vertical translations of functions. At the same time, you should have noticed the effect of those geometric patterns on the parameters in the algebraic representions of those functions. You also investigated vertical compressions and stretches of functions, and how parameters in equations affect those changes.
In this section, you will investigate how vertical reflections of functions affect the equations of those functions.
![]() Four functions, four graphs and four descriptions of transformations are listed below. Some have already been placed in the table. Place the remaining objects next to their corresponding counterparts.
Four functions, four graphs and four descriptions of transformations are listed below. Some have already been placed in the table. Place the remaining objects next to their corresponding counterparts.
Interactive popup. Assistance may be required.
The sign of the parameter, a, can create a reflection across a horizontal axis. In this case, if a < 0, then the graph of the function is reflected across the x-axis.
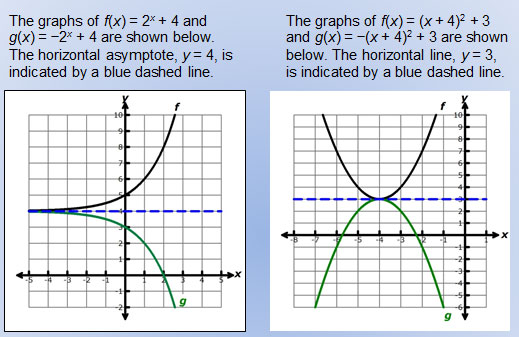
If a function has been vertically translated, how does the line of reflection relate to the vertical translation?

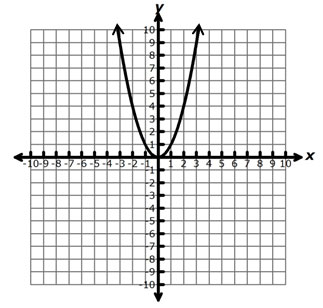
If the graph was reflected across the line y = 0, what would be the equation of the new function?
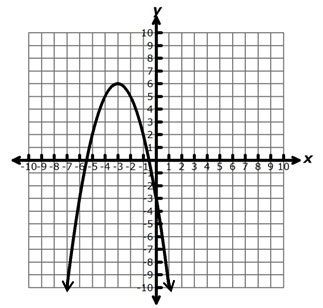
If the graph were reflected across the line y = 6, what would be the equation of the new function?
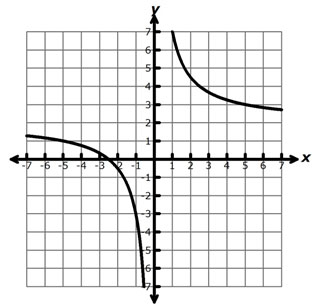
If this graph were reflected across the line y = 2, what would be the equation of the new function?