In this lesson, you are going to identify the type of conic section that a given equation represents by examining the parameters of the equation.

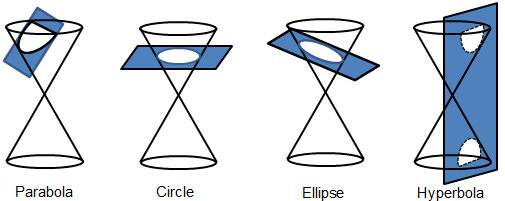
A conic section is the intersection of a plane and a right circular cone. There are four basic types of conic sections: parabolas, ellipses, circles, and hyperbolas. You already discussed parabolas and circles in previous courses, but here we'll define them a new way. Study the figures below to see how a conic is geometrically defined.

Each of the four conic sections begins with the intersection of a plane with a double-napped cone (two cones generated by rotating a line about a point, which becomes the apex of each of the two cones).

In a parabola, the plane intersects one cone parallel to the slant height of the cone.

In a circle, the plane intersects one cone parallel to the base of the cone.

In an ellipse, the plane intersects one cone at an angle between being parallel to the base and being parallel to the slant height of the cone.

In a hyperbola, the plane intersects both cones, usually at an angle greater than being parallel to the slant height.

In the conic sections above, it is important to note that the plane does not pass through the apex of the cones. When the plane does intersect the apex of the cones, the resulting conic section is called a degenerate conic section, which may include a point, a line, and two intersecting lines. This lesson does not address degenerate conic sections.