Now that you have mastered parameter changes for parabolas in the form y = x², let's change our focus on sideways parabolas in the form x = y².

The parameter changes for a sideways parabola will be similar to the ones you have already practiced. We will use the form:

x = a (y – k)² + h

Remember – whenever the equation is in this form, and the y-term is being squared, the graph is a parabola that opens left or right.

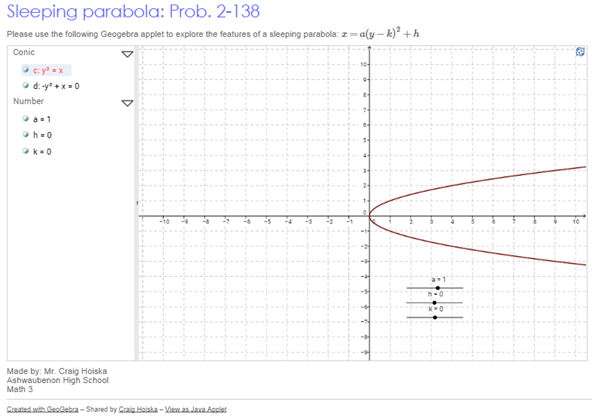
The Effects of a

• Change the value of the slider for the a parameter.
• What happens when it changes from positive to negative?
Interactive popup. Assistance may be required.
Check Your Answer
The graph reflects over the y-axis.
• What happens when a becomes more and more positive?
Interactive popup. Assistance may be required.
Check Your Answer
The parabola appears to get skinnier.
• What happens when a becomes more and more negative?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is reflected over the y-axis and appears to get skinnier.

The Effects of h and k

• Click the RESET button (the double circular arrows in the top right corner of the interactive).


• Change the value of the slider for the h parameter.


• What happens when h changes from 0 to a positive value?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is translated (shifted) to the RIGHT.
• What happens when h changes from 0 to a negative value?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is translated (shifted) to the LEFT.
• Click the RESET button (the double circular arrows in the top right corner of the interactive).
• Change the value of the slider for the k parameter.
• What happens when k changes from 0 to a positive value?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is translated (shifted) UP.
• What happens when k changes from 0 to a negative value?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is translated (shifted) DOWN.

Now that you have studied those parameter changes, it's important to note a few details.

The equation is generalized as x = a (y – k)² + h. The h-value is still associated with x and with horizontal translations. When hwas positive, the graph shifted left. When h was negative, the graph shifted right.

Likewise, the k-value is still associated with y and vertical translations. When k was positive, the graph shifted up. When k was negative, the graph shifted down. And the a-value still affects the direction the graph opens (positive to the right and negative to the left) and the width of the parabola. As a gets larger and larger, the parabola appears to get skinnier and skinnier.

Check Your Understanding

1. If you have the equation x + 5 = (y – 9)², where will the vertex of the parabola be?
Interactive popup. Assistance may be required.
Check Your Answer
The vertex will be at the point (–5, 9).
2. What is the vertex for the parabola defined as x – 200 =
   This text is hidden. Fraction: numerator two, denominator five.
   2 5 (y + 160)²?
Interactive popup. Assistance may be required.
Check Your Answer
The vertex will be at the point (200, –160).
3. Where will the vertex be for the equation x – 3 = –
   This text is hidden. Fraction: numerator one, denominator five.
   1 5 y²? Which way will the graph open? Why? Will it be narrower or wider than the graph of x = y²? Why?
Interactive popup. Assistance may be required.
Check Your Answer
This equation is equivalent to x – 3 = –
This text is hidden. Fraction: numerator one, denominator five.
1 5 (y – 0)², so the vertex will be at the point(3, 0). And since the a-value is –
This text is hidden. Fraction: numerator one, denominator five.
1 5 , it will open LEFT and appear wider than the graph of x = y².
4. What is the equation of the parabola that opens left with a =
   This text is hidden. Fraction: numerator four, denominator three.
   4 3 and its vertex at the point (15, –12)?
Interactive popup. Assistance may be required.
Check Your Answer
The equation will be x – 15 =
This text is hidden. Fraction: numerator four, denominator three.
–4 3 (y – (–12))², which would simplify to x – 15 =
This text is hidden. Fraction: numerator four, denominator three.
–4 3 (y + 12)². Notice the a-value is negative since we are told the parabola opens left.