Let's first focus our attention on y = x². Let's look at how to transform the graph of this parabola.

The graph can be changed by changing the parameters a, h, and k in the equation y = a(x – h)² + k.

You can:

• translate (shift) the graph left or right
• translate (shift) the graph up or down
• reflect the graph over the x-axis
• vertically stretch or compress the graph to make it appear narrower or wider

We are going to look at those parameter changes in the activity below. Notice that in this equation, the x-term is still being squared. Remember - whenever the equation is in this form, and the x-term is being squared, the graph is a parabola that opens up or down.

Look at this form of a parabola:

y = a (x – h)² + k

The k-value is moved to the left side of the equation. This resource is going to use the form throughout.

Click on the image below to begin the interactive exercise. Follow the instructions below.

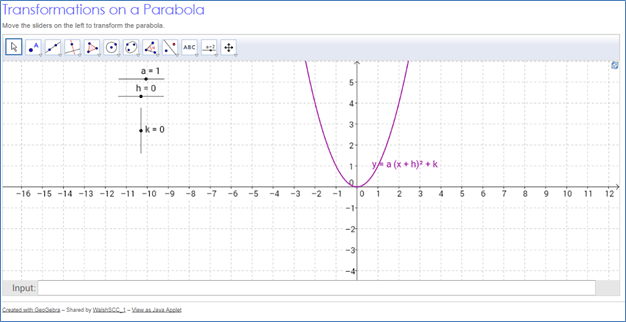
The Effects of a

• Change the value of the slider for the a parameter.
• What happens when it changes from positive to negative?
Interactive popup. Assistance may be required.
Check Your Answer
The graph reflects over the x-axis.
• What happens when a becomes more and more positive?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is vertically stretched and appears to get skinnier.
• What happens when a becomes more and more negative?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is reflected over the x-axis and is vertically stretched, appearing to get skinnier.

The Effects of h and k

• Click the RESET button (the double circular arrows in the top right corner of the interactive).
  
  
• Change the value of the slider for the h parameter.
  
  
• What happens when h changes from 0 to a positive value?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is translated (shifted) to the RIGHT.
• What happens when h changes from 0 to a negative value?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is translated (shifted) to the LEFT.
• Click the RESET button (the double circular arrows in the top right corner of the interactive).
• Change the value of the slider for the k parameter.
• What happens when k changes from 0 to a positive value?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is translated (shifted) UP.
• What happens when k changes from 0 to a negative value?
Interactive popup. Assistance may be required.
Check Your Answer
The graph is translated (shifted) DOWN.

Now that you have reviewed those parameter changes, it's important to note a few details. The equation is generalized as y = a (x – h)² + k. When h was positive, the graph shifted left. When h was negative, the graph shifted right. Likewise, when k was positive, the graph shifted up. When k was negative, the graph shifted down.

Check Your Understanding

• If you have the equation y – 2 = (x – 3)², where will the vertex of the parabola be?
Interactive popup. Assistance may be required.
Check Your Answer
The vertex will be at the point (3, 2).
• What is the vertex for the parabola defined as y + 8 = (x + 20)²?
Interactive popup. Assistance may be required.
Check Your Answer
The vertex will be at the point (-20, -8).
• Where will the vertex be for the equation y = 4 (x – 2.5)²? Which way will the graph open? Why? Will it be narrower or wider than the graph of y = x²? Why?
Interactive popup. Assistance may be required.
Check Your Answer
This equation is equivalent to y + 0 = 4 (x – 2.5)², so the vertex will be at the point (2.5, 0). And since the graph is vertically stretched by a factor of 4 (the a-value), it will open UP and appear skinnier than the graph of y = x².
• What is the equation of the parabola that opens down with a vertical compression of
  This text is hidden. Fraction: numerator one, denominator three.
  1 3 with its vertex at the point (-9, 5)?
Interactive popup. Assistance may be required.
Check Your Answer
The equation will be y – 5 = –
This text is hidden. Fraction: numerator one, denominator three.
1 3 (x – (–9))², which would simplify to y – 5 = –
This text is hidden. Fraction: numerator one, denominator three.
1 3 (x + 9)² . Notice the a-value is negative since we are told the parabola opens down.