In this lesson, you will examine several ways different types of functions and conic sections intersect graphically.  

By looking at the graph and finding the intersections you are finding the number of possible solutions for the systems of equations. Note: Not all intersections are reasonable solutions, but they all are possible solutions.

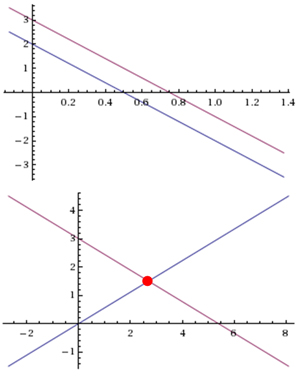
First, look at the graphs below to determine the number of ways linear functions can intersect.

Example 1:  Never (if they are parallel, causing no solution or no intersection.) –
Example 2: Once (they intersect at one point)
Example 3:Infinite number of times (if the two graphs are exactly the same).

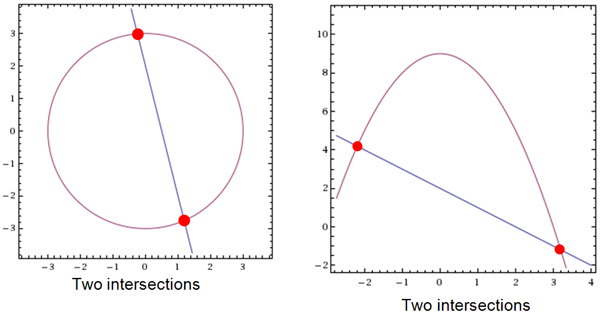
What is the maximum number of times one linear and one non-linear function can intersect? Let’s look at the graphs.  

(As you look at each graph below think about other ways the graphs could possibly intersect or even not intersect.)

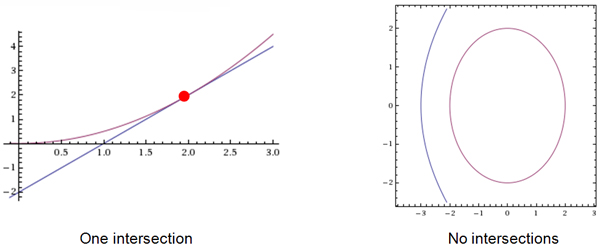
How many ways can two non-linear functions intersect? It depends on the types of graphs. Let’s look at some different types of graphs.

Review solutions to systems of equations

If a system of equations has a solution at (3,4), this simply means the graphs of the equations intersect once at the point (3,4).

1. What does it mean graphically if your system of equations has exactly two solutions: (3, 4) and (5, 8)?
   
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   The graphs would intersect exactly twice.


2. What does it mean graphically if your system of equations has no solutions?
   
   
   Interactive popup. Assistance may be required.

   Check Your Answer

   The graphs do not intersect.


3. What does it mean graphically if your system of equations has an infinite number of solutions?
   Interactive popup. Assistance may be required.

   Check Your Answer

   The graphs are identical and intersect at every single point.