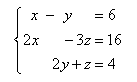Additional Practice Solving a System of Three Equations with Three Variables

If you feel like you still need practice, work some of the problems below. It may be helpful to review your notes before you start.

You will need paper to write out your solution.

Practice 1: Solve the following system of equations algebraically.

Interactive popup. Assistance may be required.

Check Your Answer

Step 1 - Solve equation 1 for x:
x - y = 6
x = 6 + y

Step 2 - Plug equation 1 into equation 2 and simplify:
2x - 3z = 16
2(6 + y) - 3z = 16
12 + 2y - 3z = 16
2y - 3z = 4

Step 3 - Subtract this result from equation 3 to eliminate y:
2y + z = 4
- (2y - 3z = 4)
0y + 2z = 0
2z = 0
z = 0

Step 4 - Plug this result into equation 2 and solve:
2x - 3z = 16
2x - 3(0) = 16
2x = 16
x = 8

Step 5 - Plug z = 0 into equation 3 and solve:
2y + z = 4
2y + 0 = 4
2y = 4
y = 2

Final solution:
(8, 2, 0)

Practice 2: Solve the following system of equations algebraically.

Interactive popup. Assistance may be required.

Check Your Answer

Step 1 - Add equation 2 and equation 3 to eliminate the x:
-2x + 2y - 3z = 4
+ 2x - 4y + z = -7
0x - 2y - 2z = -3
-2y - 2z = -3

Step 2 - Multiply each side of equation 1 by 2 and add the result to equation 2 to eliminate the x:
2 x (x + 2y - z = -3)
2x + 4y - 2z = -6
+ -2x + 2y - 3z = 4 (equation 2)
0x + 6y - 5z = -2
6y - 5z = -2

Step 3 - Multiply the equation from step 1 by 3 and add it to the equation from step 2 to eliminate the y:
3x (-2y - 2z = -3)
-6y - 6z = -9
+ 6y - 5z = -2 (step 2 result)
0y - 11z = -11
-11z = -11
z = 1

Step 4 - Plug z = 1 into equation from step 1 and solve:
-2y - 2z = -3
-2y - 2(1) = -3
-2y - 2 = -3
-2y = -1
y = 1 over 2 1 2 ,1)

Step 5 - Plug y = 1 over 2 1 2 ,1) and z = 1 into equation 1:
x + 2y - z = -3
x + 2( 1 over 2 1 2 ,1) - 1 = -3
x +1 - 1 = -3
x = -3

Final solution
(-3, 1 over 2 1 2 ,1)

Practice 3: Solve the following system of equations algebraically.

Interactive popup. Assistance may be required.

Check Your Answer

Step 1 - Add equation 1 to equation 2 to eliminate the z:
x + y - z = 6
+ 3x - 2y + z = -5
4x - y + 0z = 1
4x - y = 1

Step 2 - Multiply equation 1 by 2 and add then subtract equation 3 to eliminate the z:
2 x (x + y - z = 6)
2x + 2y - 2z = 12
- (x + 3y - 2z = 14)
x - y + 0z = -2
x - y = -2

Step 3 - Solve this equation for x:
x - y = -2
x = y - 2

Step 4 - Plug this equation into the result of step 1 and solve for y:
4x - y = 1
4(y - 2) - y = 1
4y - 8 - y = 1
3y - 8 = 1
3y = 9
y = 3

Step 5 - Plug y = 3 into step 3 and solve for x:
x = y - 2
x = 3 - 2
x = 1

Step 6 - Plug x = 1 and y = 3 into equation 1 and solve for z:
x + y - z = 6
1 + 3 - z = 6
4 - z = 6
z = -2

Final Solution
(1,3,-2)