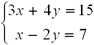
Solve by graphing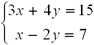 

Solution:

1. Translate both equations into a calculator-friendly form. This form could be slope-intercept form, which is most familiar to you, or it could be just one step short of slope-intercept form. If you need to review how to do solve for y, click Interactive popup. Assistance may be required. here for the steps.

Solve for y:

2. Write the two equations in the calculator.

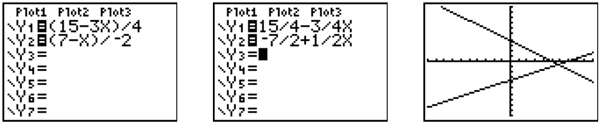
3. Now, you want CALC which you can get from 2nd TRACE.

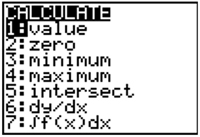
4. Select intersect.

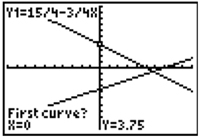
5. Move the cursor close to the point of intersection and press enter for “First curve?” and “Second curve?” and “Guess?”. Then you should see the coordinates for the point of intersection/solution.

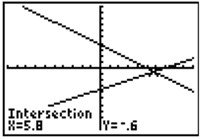
The solution of this system is (5.8, -0.6). These coordinates would have been very difficult to determine from looking at the graph alone.