In the previous section, you used inequalities or verbal descriptions to indicate the domain and range of functions. In order to standardize communication among mathematicians, scientists, and engineers - as well as other people who use mathematics - notation, or an agreed-upon way to write a particular idea, is important. Much like how teenagers developed a notation for sending text messages (LOL, OMG, TTYL, etc.), mathematicians developed several ways to compactly send messages to one another about domain and range.
Interval notation eliminates the familiar < or > symbols used for inequalities and replaces them with brackets. Parenthesis, or ( and ) are used to indicate "less than but not including" and "greater than but not including." Hard brackets, or [ and ] indicate "including," or "or equal to."
| Inequality | Interval |
|---|---|
| < | ) |
| > | ( |
| ≤ | ] |
| ≥ | [ |
Unlike inequalities, interval notation requires two endpoints. If only one limit is known, then the other one is indicated using infinity, ∞. For interval notation, infinity is always accompanied by a parenthesis rather than a hard bracket.
![]() Drag each inequality to it's correct place in the chart below.
Drag each inequality to it's correct place in the chart below.
You can see from the examples in the table, interval notation is much more compact than inequality notation!
Set notation is used to indicate the domain and range as a set of numbers. Though not as compact as interval notation, it is a way that mathematicians use to convey two important pieces of information: what types of numbers are included in the set (real numbers, integers, etc.), and which of those numbers are excluded from the set.
For example,
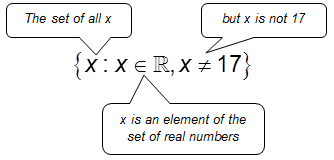
The set notation above contains three important pieces of information, and is mathematical shorthand for "the set of all x such that x is an element of the set of real numbers, and x is not equal to 17." Much more compact! The punctuation separates the three distinct ideas. The colon is used to transition from the first two pieces of information and is read, "such that." The comma indicates that an exception or a clarifier to the second piece of information is coming.
Let's revisit the table from Section 1 of this resource.
![]() The table below contains several functions that you will encounter in Algebra 2. Drag each function to its correct place in the table.
The table below contains several functions that you will encounter in Algebra 2. Drag each function to its correct place in the table.