When you are asked to find the domain and range from the graph of a function given the equation, it will be easier to see why the graph looks a certain way and what kind of function is graphed. In other words, the characteristics for the function will be similar to the parent function.

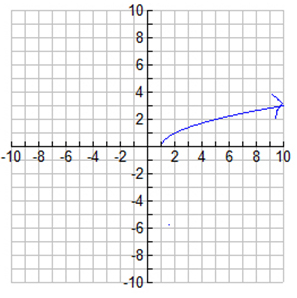
graph of a curved line in the first quadrant with starting point at x=1 and y=0 with graph continuing to infinity on the left

For example, the graph of the function pictured above should indicate to you that it is not a linear (y = mx + b) function because this is not the graph of a line which would show the domain and range to be all real numbers. All linear function domains and ranges are always all real numbers.

It is not a quadratic function (y = x2) because it is not a parabola.

This is the graph of the radical equation √x − 1. Since the graph begins at (1,0), this tells us the beginning points of the domain and range. The domain is { x| x ≥ 1 }which is read as "the set of all x's such that x is greater than or equal to 1." The range is { y| y ≥ 0 } which is read as "the set of all y's such that y is greater than or equal to zero." This notation is called set builder notation.