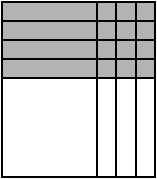
This section puts all the information together to solve a quadratic based on the configuration of the algebraic tiles.
Example: Solve x2 − x − 12 = 0.
The tile diagram would look like
The factors are (x − 4)(x + 3)
Since we are solving the equation, set the product equal to zero.
(x − 4)(x + 3) = 0
To solve (x + 3) (x − 4) = 0, set each factor equal to 0.
x + 3 = 0
-3 -3
x = -3
and
x − 4 = 0
+4 +4
x = 4
The solution to the equation x2 − x − 12 = 0 is x = -3 and x = 4.
If x is replaced in the original equation with -3, the equation is true.
(-3)2 − (-3) − 12 = 0 |
9 + 3 − 12 = 0 |
0 = 0 |
If x is replaced in the original equation with 4, the other value for x, the equation is true.
(4)2 − (4) − 12 = 0 |
16 − 4 − 12 = 0 |
0 = 0 |
Example: Solve for x:
First, rewrite the equation so that it equals 0.
The new equation is 6x2 + 7x + 2 = 0.
Now, watch as tiles are used to create a diagram.
The factors are Interactive popup. Assistance may be required.
(2x + 1)(3x + 2)
Write the equation using the factors. Interactive popup. Assistance may be required.
(2x + 1)(3x + 2) = 0
Solve (2x + 1)(3x + 2) = 0 by setting each factor equal to 0.
2x + 1 = 0
-1 − 1
2x 2 = -1 2
x = -1 2
and
3x + 2 = 0
-2 - 2
3x 3 = -2 3
x = -2 3
The solution to the equation 6x2 + 7x + 2 = 0 is x = − 1 2 and x = - 2 3.