Watch the video below. As you do so, notice the parabolas being created by the experimenters.

Use what you have seen in the video to drag the key vocabulary words to the appropriate blanks in the paragraph that follows. Press the reset button, if you need to reset the interactive.

In the experiment you watched in the video, different heights of the tables affected the graphs of the parabolas. The graphs of the quadratic functions shown below are all graphed on the same set of axes. Match the graph to a possible description of the graph.

Pause and Reflect

How can you tell if a vertex will be a maximum or a minimum for the parabola?

Interactive popup. Assistance may be required.

Check Your Answer

If the parabola opens upward, the vertex is a minimum. If the parabola opens downward, the vertex is a maximum.

If the value of a remains the same, and the vertex moves upward, what will happen to the y-intercept of the parabola?

Interactive popup. Assistance may be required.

Check Your Answer

If the value of a remains the same, the y-intercept will move the same number of units upward as the vertex.

Practice

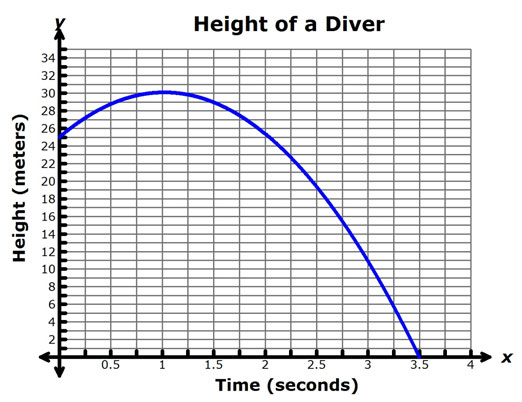
The graph below represents the height of a diver versus the time after the diver jumps from a springboard. Use the graph below to answer questions 1-4.

1. Is the vertex of the graph a maximum or a minimum point for the parabola? How can you tell?

   Interactive popup. Assistance may be required.

   Need a hint?

   Are the remaining y-values in the parabola less than or greater than the y-value of the vertex?

   Interactive popup. Assistance may be required.

   Check Your Answer

   Maximum

2. What are the coordinates of the vertex?

   Interactive popup. Assistance may be required.

   Need a hint?

   Estimate the location of the maximum or minimum value of the parabola.

   Interactive popup. Assistance may be required.

   Check Your Answer

   (1, 30)

3. What does the vertex of the graph represent?

   Interactive popup. Assistance may be required.

   Need a hint?

   Use the labels of the axes to interpret the values of the x- and y-coordinates.

   Interactive popup. Assistance may be required.

   Check Your Answer

   One second after leaving the diving board, the diver reaches a maximum height of approximately 30 meters.

4. Is the value of a in this equation positive or negative? How can you tell?

   Interactive popup. Assistance may be required.

   Need a hint?

   Does the graph open upward or downward?

   Interactive popup. Assistance may be required.

   Check Your Answer

   The value of a is negative because the graph opens downward.