In this resource, you will analyze the graphs of quadratic functions. In the first section, you will focus on the direction in which a parabola opens and the width of the parabola itself.

This is exciting! A smile is forming on your face.

The smile on your face could be considered a possible graph of a quadratic function. Click on the graph below.

• In which direction do both parabolas in the graph open?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Both parabolas open upward.

• What does the direction in which the parabolas tell you about the sign of the value of a in the function y = ax² that would generate each parabola?

  Interactive popup. Assistance may be required.

  Check Your Answer

  Because both parabolas open upward, the sign of the value of a in the function generating each parabola is positive.

• How does the parabola representing the smile compare to the original parabola, which is the quadratic parent function, y = x²?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The parabola representing the smile is more narrow than the parent function.

• How does the value of a in the function y = ax² for the parabola representing the smile compare to the value of a for the parent function, y = x²?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The value of a for the parabola representing the smile is greater than 1 and is greater than the value of a for the parent function.

• Is the vertex for each parabola a minimum value or a maximum value? How can you tell?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The vertex for each parabola is a minimum value because the y-value for the vertex is less than the y-values for the remaining points on each parabola.

Place the four smiles in order from the least value of a to the greatest value of a. Drag and drop each smile to its appropriate place.

View the animation below to see parabolas in a famous marketing symbol. Click on the words "famous landmark" to start the animation, and then use the animation to answer the questions that follow.

• In what direction do the parabolas in the "Golden Arches" symbol appear to open?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The parabolas open downward.

• If you were to write an equation representing each parabola in the "Golden Arches," would the value of a be positive or negative? How do you know?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The value of a would be negative because the parabolas open downward.

• Are the vertices for each parabola in the "Golden Arches" maximum values or minimum values? How do you know?

  Interactive popup. Assistance may be required.

  Check Your Answer

  The vertices are maximum values because all other y-values in each parabola would be less than the vertex at the top of the arch.

Practice

The graphs below are all of the form y = ax².

1. Which of the graphs have a value of a < 0?

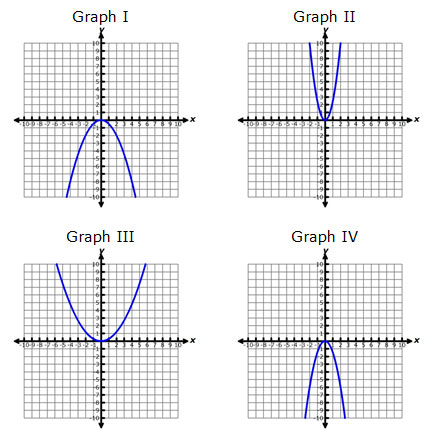
   Interactive popup. Assistance may be required.

   Need a hint?

   If the value of a is less than 0, will the graph open upward or downward?

   Interactive popup. Assistance may be required.

   Check Your Answer

   Graphs I and IV

2. Which graph appears to have the largest |a|?

   Interactive popup. Assistance may be required.

   Need a hint?

   Which graph appears to be the narrowest?

   Interactive popup. Assistance may be required.

   Check Your Answer

   Graph II

3. List the graphs in order from the greatest value of a to the least value of a.

   Interactive popup. Assistance may be required.

   Need a hint?

   The narrowest graph that opens upward will have the greatest value of a, and the narrowest graph that opens downward will have the least value of a.

   Interactive popup. Assistance may be required.

   Check Your Answer

   Graph II, Graph III, Graph I, Graph IV