Sometimes, you will be presented a problem in verbal form rather than in symbolic form. In order to determine the domain and range of a quadratic function in verbal form, it is often easier to use the verbal representation—or word problem—to generate a graph. Then, you can find the domain and range from the graph more easily.

Click on the image to access the video.

.

• Watch the video. When asked to identify the true statement regarding the independent and dependent variable, choose A, B, or C.
• Record the example problem and the table of values for t and h.
• After the graph is drawn, identify the domain and range for the function and record it in your notes. Estimate the maximum value of t for the domain.

For the following examples, use your graphing calculator or an online graphing calculator, such as the one available at Graphing Calculator, to graph the functions and determine the domain and range of the quadratic function from its graph.

Example 4

A bird is building a nest in a tree 30 feet above the ground. The bird dropped a stick from the nest. The function f(x) =  -16x² + 36 describes the height of the stick in feet after x seconds. The graph of this function is shown below. Identify the domain and range of this function.

Pause and Reflect

Why is the domain and range for a situation like this restricted to Quadrant I, when the graph of the function modeling the situation continues into other quadrants?

Possible Response

In this situation, it does not make sense for values of x or y to be negative. Thus, we only use the portion of the quadratic function whose graph appears in Quadrant I to model the situation.

Example 5

The DeWind family lives in a rectangular shaped home with a length of 45 feet and a width of 35 feet. Mr. DeWind plans to install carpet in every room of the house with the exception of the square kitchen. The kitchen has a side length of x feet and the function y = 1575 − x² describes the area of the home, without the kitchen, in square feet. Identify the domain and range of this function.

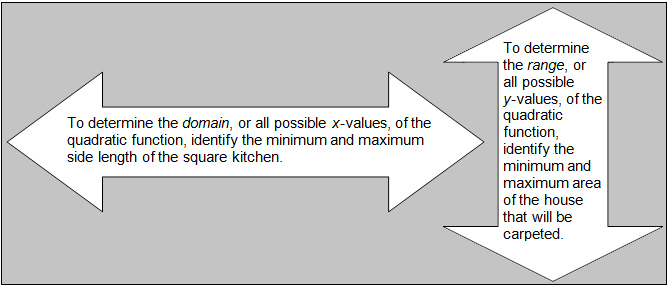
What is the domain for this situation?

Need a hint (Domain)?

The side length of the kitchen must be less than the width of the house but greater than 0.

Check Your Answer (Domain)

Domain: 0 < x < 35, or all real numbers between, but not including, 0 and 35.

What is the range for this situation?

Need a hint (Range)?

As the side length of the kitchen increases from 0 to 35, the area of the carpeted portion of the home decreases from 1575 to 350.

Check Your Answer (Range)

Range: 350 < y < 1575, or all real numbers between, but not including, 350 and 1575.

Example 6

A student launches a model rocket. The height of the rocket, h, in feet after t seconds is given by the function
h = -16 t² + 16t + 4. Identify the range of this function.

To determine the range, graph the function.

See a Graph

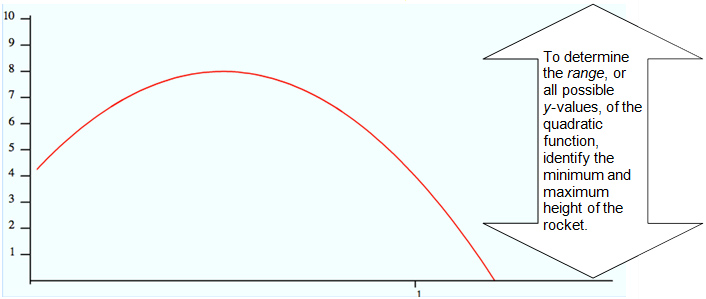
What is the range for this situation?

Need a hint (Range)?

The minimum height of the rocket is 0 when the rocket reaches the ground. The maximum height of the rocket is 8.

Check Your Answer (Range)

Range: 0 ≤ y ≤ 8, or all real numbers between, and including, 0 and 8.