In this section bacteria and population exponential problems are examined. A graphing calculator is needed.

Example: In biology, bacteria cultures grow according to exponential growth. One biologist noticed that the population of bacteria in a sample doubled every four days. The biologist needs to create an equation to be able to determine the exponential growth of the bacteria.

Fill in the following blanks.

Click on the blanks to reveal the answers.

• When writing an equation, the biologist needs to know the Interactive button. Assistance may be required. ____ initial amount of bacteria and the rate of Interactive button. Assistance may be required. ____ growth .
• The original amount of bacteria is Interactive button. Assistance may be required. ____ a , and the rate of growth is the base Interactive button. Assistance may be required. ____ b .

Examine the equations below. Select the one representing the bacteria growth. After selecting the equation, read the explanations provided for each equation below.

1. y = 10 (2)^x
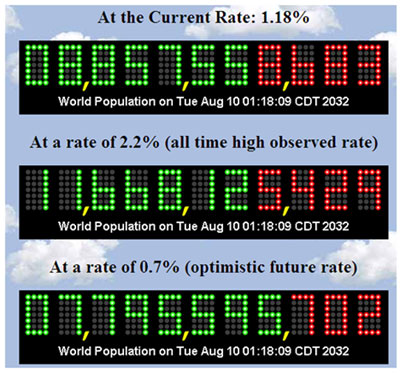
   • The Interactive button. Assistance may be required. ____ 10 in this equation represents the Interactive button. Assistance may be required. ____ initial amount of bacteria, and the rate of Interactive button. Assistance may be required. ____ growth .
   • The 2 represents the bacteria Interactive button. Assistance may be required. ____ a or Interactive button. Assistance may be required. ____ b.
   • The x represents the time it takes the bacteria to Interactive button. Assistance may be required. ____ double.

     Put the equation in a graphing calculator and graph. Review the table of the graph below.

     

   • According to the table, the sample Interactive button. Assistance may be required. ____ does not double in Interactive button. Assistance may be required. ____ 4 days therefore this equation Interactive button. Assistance may be required. ____ does not fit the information given.
2. y = (4)x over 10 x 10
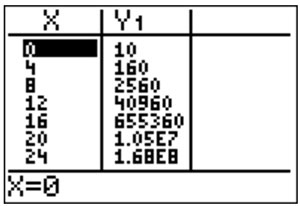
   • The Interactive button. Assistance may be required. ____ 1 in this equation (there isn't a number in front of the (4) therefore there is a 1), represents the Interactive button. Assistance may be required. ____ initial amount of bacteria, Interactive button. Assistance may be required. ____ a.
   • The 4 represents the bacteriaInteractive button. Assistance may be required. ____ quadrupling or Interactive button. Assistance may be required. ____ b.
   • The x 10 represents the time it takes the bacteria to Interactive button. Assistance may be required. ____ quadruple every Interactive button. Assistance may be required. ____ 10 days.
   • This equation Interactive button. Assistance may be required. ____ does not fit the information given, since it Interactive button. Assistance may be required. ____ quadruples every Interactive button. Assistance may be required. ____ 10 days instead of doubling every Interactive button. Assistance may be required. ____ 4 days.
3. y = 10(2)x over 4 x 4
   • The Interactive button. Assistance may be required. ____ 10 in this equation represents the Interactive button. Assistance may be required. ____ initial amount of bacteria, Interactive button. Assistance may be required. ____ a.
   • The 2 represents the bacteria Interactive button. Assistance may be required. ____ doubling or Interactive button. Assistance may be required. ____ b.
   • The x 4 represents the bacteria Interactive button. Assistance may be required. ____ doubling every Interactive button. Assistance may be required. ____ 4 days.

     Put the equation in a graphing calculator and graph. Review the table of the graph below.

     

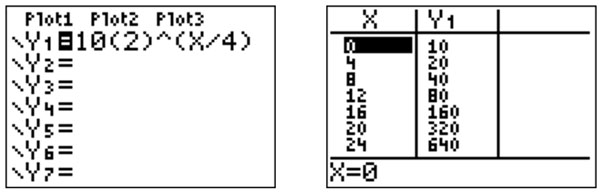
   • This equation Interactive button. Assistance may be required. ____ does fit the information given since it Interactive button. Assistance may be required. ____ doubles every Interactive button. Assistance may be required. ____ 4 days.
4. y = 10 (4)^x
   • The Interactive button. Assistance may be required. ____ 10 in this equation represents the Interactive button. Assistance may be required. ____ initial amount of bacteria, Interactive button. Assistance may be required. ____ a.
   • The 4 represents the bacteria Interactive button. Assistance may be required. ____ quadrupling or Interactive button. Assistance may be required. ____ b.
   • The x represents the time it takes the bacteria toInteractive button. Assistance may be required. ____ quadruple.

     Put the equation in a graphing calculator and graph. Review the table of the graph below.

     

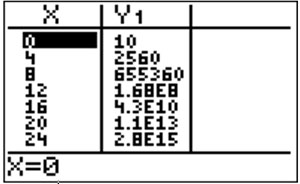
   • According to the table, the sample Interactive button. Assistance may be required. ____ does not double in Interactive button. Assistance may be required. ____ 4 days; therefore, this equation Interactive button. Assistance may be required. ____ does not fit the information given.

Example: Egypt’s current population is approximately 80 million with a growth rate of 2%. Create an equation to represent the relationship between the population of Egypt, E, and the number of years, t, from this year.

Examine the equations below. Select the one representing the population of Egypt. After selecting the equation, read the explanations provided.

1. E = 80,000,000 (2)^t
   • The Interactive button. Assistance may be required. ____ 80,000,000 in this equation represents the Interactive button. Assistance may be required. ____ initial population, Interactive button. Assistance may be required. ____ a.
   • The 2 represents the population Interactive button. Assistance may be required. ____ doubling or Interactive button. Assistance may be required. ____ b.
   • The t represents the time it takes the population to Interactive button. Assistance may be required. ____ double.
   • This equation Interactive button. Assistance may be required. ____ does not fit the information given since the population’s growth rate is Interactive button. Assistance may be required. ____ 2%, it Interactive button. Assistance may be required. ____ does not double.
2. E = 80,000,000 (0.02)^t
   • The Interactive button. Assistance may be required. ____ 80,000,000 in this equation represents the Interactive button. Assistance may be required. ____ initial population, Interactive button. Assistance may be required. ____ a.
   • The 0.02 represents the population's growth rate Interactive button. Assistance may be required. ____ b.
   • The equation is an exponential Interactive button. Assistance may be required. ____ decay equation because Interactive button. Assistance may be required. ____ b is less than Interactive button. Assistance may be required. ____ 1.
   • This equation Interactive button. Assistance may be required. ____ does not fit the information given since the equation is an exponential Interactive button. Assistance may be required. ____ decay equation.
3. E = 80,000,000 (0.98)^t
   • The Interactive button. Assistance may be required. ____ 80,000,000 in this equation represents the Interactive button. Assistance may be required. ____ initial population, Interactive button. Assistance may be required. ____ a.
   • The 0.98 represents the population growth rate Interactive button. Assistance may be required. ____ b.
   • The equation is an exponential Interactive button. Assistance may be required. ____ decay equation because Interactive button. Assistance may be required. ____ b is less than Interactive button. Assistance may be required. ____ 1.
   • This equation Interactive button. Assistance may be required. ____ does not fit the information given, since the equation is an exponential Interactive button. Assistance may be required. ____ decay equation where the population is Interactive button. Assistance may be required. ____ decreasing by 2%.
4. E = 80,000,000 (1.02)^t
   • The Interactive button. Assistance may be required. ____ 80,000,000 in this equation represents the Interactive button. Assistance may be required. ____ initial population, Interactive button. Assistance may be required. ____ a.
   • The 1.02 represents the population Interactive button. Assistance may be required. ____ b.
   • The t represents the time it takes the population to Interactive button. Assistance may be required. ____ increase by 2%.
   • This equation Interactive button. Assistance may be required. ____ does fit the information given since the population's growth rate is Interactive button. Assistance may be required. ____ 2%, 100% + 2% = 102% or 1.02.

Example: Below are population projections for the year 2032 based on three difference population growth figures. Using these numbers, create an equation to calculate today's population.

• The general exponential equation is Interactive button. Assistance may be required. ____ y = ab_x.
• There are Interactive button. Assistance may be required. ____ variables, three of the four variables need to be known to solve for the fourth.
• The variable a is the Interactive button. Assistance may be required. ____ initial population, the unknown variable in this problem.
• From the screen shot below, the current growth rate is Interactive button. Assistance may be required. ____ 1.18% or Interactive button. Assistance may be required. ____ b.

Source: World Population Scenarios, Dr. Darkmatter (The Electronic Universe), University of Oregon

• The actual value for b is Interactive button. Assistance may be required. ____ . 100% + 1.18% = 101.18% or 1.0118
• The projected world population in 22 years, at the current rate, is Interactive button. Assistance may be required. ____ 8,857,558,683 people, or the variable Interactive button. Assistance may be required. ____ y.
• The equation is Interactive button. Assistance may be required. ____ a(1.0118)²².
• Solve the equation:
  
  Interactive popup. Assistance may be required.

  Check Your Answer

  8,857,558,683 = a (1.0118)²²
  
  8,857,558,683 = a (1.294442762)
  
  8,857,558,683 1.294442762 = a 1.294442762 1.294442762
  
  6,842,758,091 = a
• The actual world population is 6,861,551,655 people; the difference is because Interactive button. Assistance may be required. ____ 1.18% is a rounded number.

More Practice