This section provides an example of a common exponential growth using bacteria. A calculator is helpful.
Bacteria can multiply at an alarming rate. The exponential growth rate for bacteria is usually two; it splits into two new cells or doubles at a given rate.
Example: If at the beginning of a school day there is only one bacterium that doubles every three hours, by the end of the day how many bacteria are there?
Complete the table below.
Click on the blanks to reveal the answers.
| Time | Number of bacteria |
| 8:00 | 1 |
| 11:00 | Interactive button. Assistance may be required. ____ 2 |
| 2:00 | Interactive button. Assistance may be required. ____ 4 |
| 5:00 | Interactive button. Assistance may be required. ____ 8 |
| 8:00 | Interactive button. Assistance may be required. ____ 16 |
| 11:00 | Interactive button. Assistance may be required. ____ 32 |
Below is a graph representing this table.

NOTE: In math it’s difficult to deal with time because we have a repeating 12-hour clock. If you look at the data, you have two 8:00 with two different amounts. We understand that 8:00 am is different than 8:00 pm so often in math we change the times to 0, 1, 2, 3, etc., with the starting time as time zero.
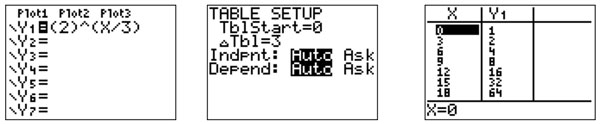
The table below changed the time to hours after the starting time.
| Time | Time (hours after start) | Number of bacteria |
| 8:00 | 0 | 1 |
| 11:00 | 3 | 2 |
| 2:00 | 6 | 4 |
| 5:00 | 9 | 8 |
| 8:00 | 12 | 16 |
| 11:00 | 15 | 32 |
The graph is the same, except the x-axis is numbered in hours instead of the time.
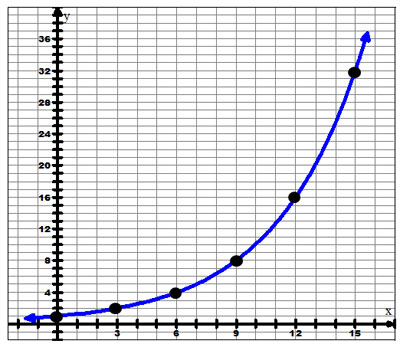
The rate of the exponential growth is Interactive button. Assistance may be required. ____ 3 since the bacteria Interactive button. Assistance may be required. ____ double every three hours. The equation of this curve is y = 2x over 3 x 3
Put the equation in your calculator and graph. Go to the calculator’s table to see if it matches the given table. They should be the same.