This section reviews the power laws, the Power of a Power, the Power of a Product Law, and the Power of a Quotient Law. Experiment with the power laws below.

 A quick review.
A quick review.
(After clicking on the link above, follow the directions below.)
- Click on “Bigger” in the upper right hand corner.
(The following images are only illustrations. Follow the link above to complete the activity.) 
- Click on the third box
 to practice the Power of a Power Law.
to practice the Power of a Power Law.
- The m-value (purple), n-value (orange), and x-variable are changed by moving your cursor to the left or right on the purple, orange or red number line.
- Select different values for m-, n-, and x–values. Each time a new value is selected, the Law is demonstrated and the answer is shown at the bottom.
- Practice until you understand the Power of a Power Law.
- Click on the X when done practicing.
- Click on the fourth box
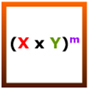 to practice the Power of a Product Law.
to practice the Power of a Product Law.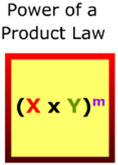
- Follow the previous directions.
- Many students get confused about the difference between the Power of a Power Law and the Power of a Product Law. Make sure that you can tell the differences between the two.
- Click on the fifth box
 to practice the Quotient of a Product Law.
to practice the Quotient of a Product Law. 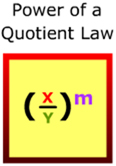
- Follow the previous directions.
Note: The Power of a Product Law and the Power of a Quotient Law only have one exponent.
In your notes, complete the following sentences and solve the problem:
- The Power of a Power Law states that when taking an exponential expression to a power, you should __________________.
Interactive popup. Assistance may be required.
Check Your Answer
- The Power of a Product Law states that when multiplying exponential expressions with the same base you should __________________.
Interactive popup. Assistance may be required.
Check Your Answer
- The Power of a Quotient Law states that when dividing exponential expressions with the same base, you should __________________.
Interactive popup. Assistance may be required.
Check Your Answer
- The side of a square is 6x3y2 feet. Find the area of the square. Hint: Use A = s2 for the formula.
Interactive popup. Assistance may be required.
Check Your Answer


 to practice the Power of a Power Law.
to practice the Power of a Power Law.
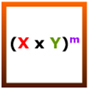 to practice the Power of a Product Law.
to practice the Power of a Product Law.
 to practice the Quotient of a Product Law.
to practice the Quotient of a Product Law. 



