Source: Algebra Tiles, 26 Design
What if one of the shapes does not zero out? You must use multiplication and addition to get one of the shapes to cancel out.
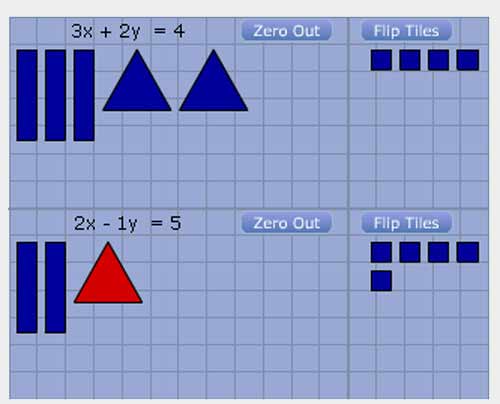
Look at this example of a system of equations.
3x + 2y = 4
2x – 1y = 5

Source: Algebra Tiles, 26 Design
Your goal is to eliminate one of the variables (rectangles or triangles). In the problem above, it looks like it would be easier to eliminate the triangles. Why? Go to your notes and explain how to eliminate the triangles using the example above. Click below to check your answer.
Interactive popup. Assistance may be required.
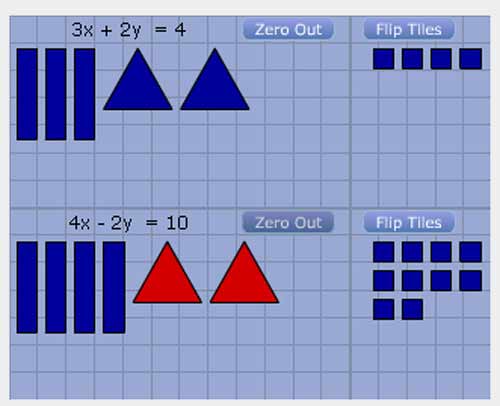
If you want to eliminate the triangles, you must have a "zero pair", meaning that you need a positive (blue) triangle and negative (red) triangle to cancel out. Notice you have 2 blue triangles on top and 1 red on the bottom. You must double (x 2) every shape in that row, giving you 4 blue rectangles, 2 red triangles, and 10 blue squares. Now you are able to put the two rows together. Please note that you may not add 1 to each of the terms because you wouldn't be adding the same shape.
IMPORTANT NOTE:
If you want to change one term of an equation, you must change all the terms to keep its equivalency.
2 + 3 = 5 (example)
2(2) + 3(2) = 5(2)
4 + 6 = 10 Equation is still equivalent.
If you don’t get all the terms…
2(2) + 3(2) = 5
4 + 6 ≠ 5 Equation is NOT equivalent.
Let's eliminate the triangles by first doubling the second row.
Source: Algebra Tiles, 26 Design
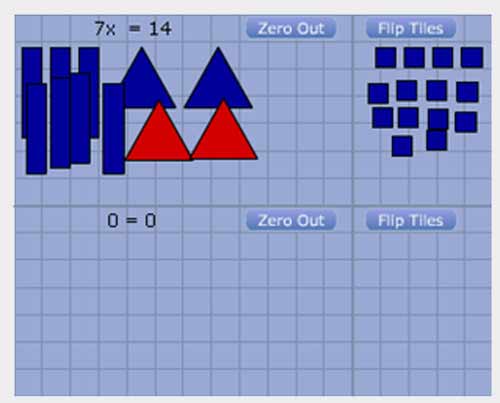
Next add the two rows together and zero out.
Source: Algebra Tiles, 26 Design
Zero out and divide by 7 to find the value of x. Read the additional information in the box to find the value of y and the solution to this system of equations.
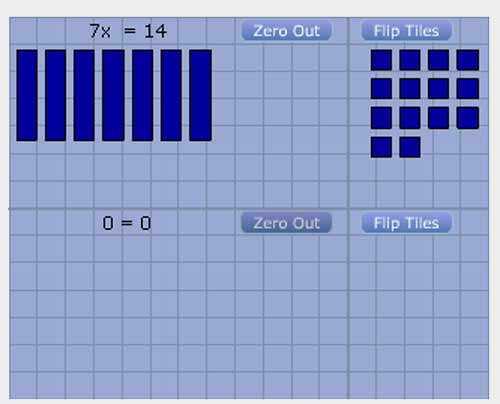
You can evenly disperse 2 squares to every rectangle, so rectangle or x = 2.
Now, go back to the original equations, pick one, substitute 2 for x.
Either equation
substitute 2 for x
evaluate
subtract from both sides
divide by 2
solution (2, -1)
Now you can practice by using the other set of equations in the applet on the website.
2x + 3y = 5
1x + 1y = 3
Go to the website and then press Check and Clear to work the other problem on the website.