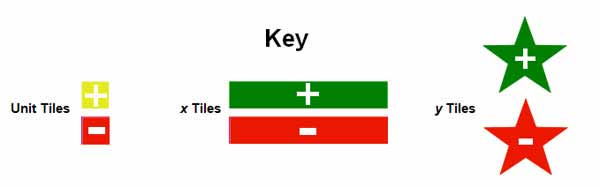
In this resource you will be solving a system of linear equations using models. Look at the key below.

In the key, the squares stand for unit values, the rectangles stand for the x values, and the stars stand for the y values. Notice when the shapes are red they represent negative values. Let's look at how the equations of two lines would be represented.

y = 4x – 5
2x + y = 1

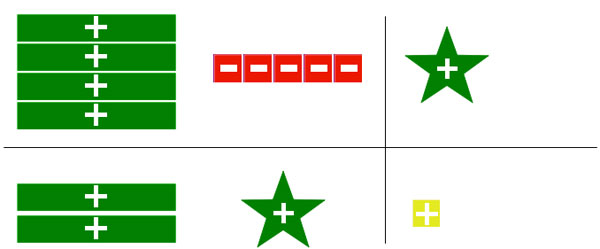
Notice that there is a horizontal line separating the two equations and a vertical line standing for the equal signs. So the first equation at the top represents y = 4x – 5 or 4x – 5 = y showing four rectangles for the x, five red squares, and one star. The second equation at the bottom shows 2x + y = 1 with two rectangles, one star, and one square.

Substitution is one way to solve a system of equations. In this system of linear equations, one of the equations has a variable isolated, y = 4x – 5. Therefore, you can use substitution to solve the system of equations.

Take the value of y, (4x – 5), and substitute it into the second equation for the value of y.

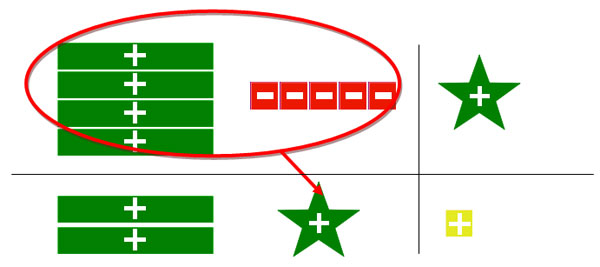
The new second equation will become 6x – 5 = 1 as shown.

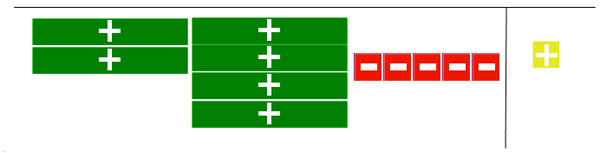
To then solve for x, you must add +5 to both sides of the equation to eliminate the -5.

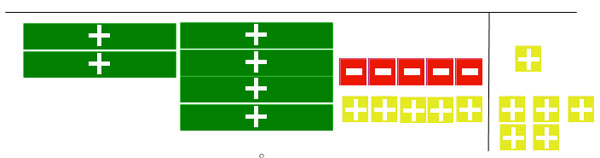
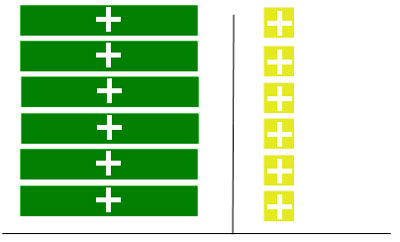
When the zero pairs are eliminated all you have left is 6x = 6, so you can line up the x's with the units and see that x = 1.

What if the question asked you to find the solution for the system of equations? Then you would need to know the x-value that you found above and the y-value. To find the y-value, you would substitute the x-value into one of the equations.

So if you take y = 4x – 5 and substitute 1 for x, you would get y = 4(1) – 5 and y would be -1. Therefore, the solution for the system of equations would be (1, -1).

Would you get the same answer if you substitute 1 for x in the other equation? Yes, you should. The second equation would be 2(1) + y = 1 and y = -1.