At times, you may be given a partial ordered pair and an equation, and you will be asked to determine the value of the missing variable.

Example: Let's say that you were told that (x, 6) is a solution to the equation 2x + 5y = 32 and you need to determine the value of x.

Algebraically, you would just need to substitute 6 for y in the equation and solve for x.

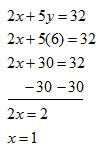
line 1: 2x + 5y = 32, line 2: 2x + 5(6) = 32, line 3: 2x + 30 = 32, line 4: substract 30 from both sides of equation, line 5: 2x = 2, line 6: x = 1

Example: If (−1, y) is a solution to the equation 2x – 7y = 40, what is value of y

This time, you would need to substitute -1 for x in the equation and solve for y.

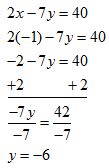
line 1: 2x - 7y = 40, line 2: 2(-1) - 7y = 40, line 3: -2 - 7y = 40, line 4: add 2 to both sides of the equation, line 5: fraction; numerator: -7y, denominator: -7 = fraction; numerator: 42, denominator: -7, line 6: y = -6

You could also enter the equation (in y = form) into your graphing calculator and look at the table of values that is generated by the equation.

For example, if we look at the equation for the last example (2x – 7y = 40) and rewrite it so that it is in y = form, the equation would be 2 7 x – 40 7 .

Enter this into your graphing calculator under Y1 and look at the TABLE for the y-value when x = -1.

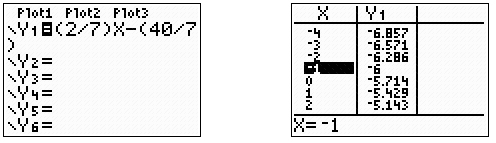
By looking at the table, we can see that when x = -1, y = -6.

Practice

Answer the following questions on your own paper.

  1. If (2, y) is a solution to the equation 5x – 2y = 8, what is the value of y?
  2. If (x, -3) is a solution to the equation x + 2y = 1, what is the value of x?
Interactive popup. Assistance may be required.

Check Your Answers

  1. y = 1
  2. x = 7
Close Pop Up