In this lesson, you extended what you know about solving one-variable inequalities and linear equations to solving linear inequalities.

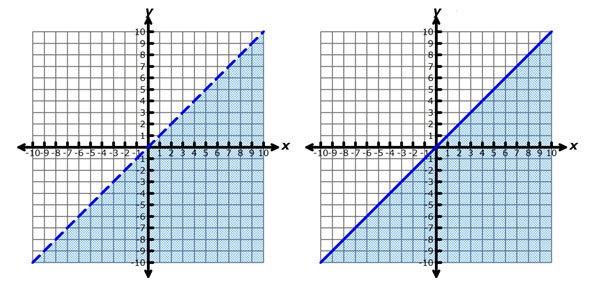
Linear inequalities may be solved graphically or symbolically using the properties of equality. In a graph, the solution set for an inequality is represented in the coordinate plane using two features: a boundary line and a shaded region.

If the boundary line is dashed, then the points along the boundary line are not included in the solution set of the inequality. If the boundary line is solid, then the points along the boundary line are included in the solution set of the inequality.

Properties of equality can also be used to solve linear inequalities. Solving linear inequalities is an algebraic process that is very similar to solving linear equations, with one additional feature. If multiplication or division by a negative number is used, the inequality symbol must be reversed in order to preserve the value of the inequality.