In this part of the lesson, you will focus on using properties of equality to solve linear inequalities that come from problem situations.

Carla and Crystal own a coffee shop. They want to create a house blend of coffee from two beans. Costa Rica Sunrise beans cost $7.50 per pound, and Colombia’s Best beans cost $8.75 per pound. They want to create a blend of beans that cost no more than $120 per batch. Carla has suggested that they use the following inequality, where x represents the number of pounds of Costa Rica Sunrise beans, and y represents the number of pounds of Colombia’s Best beans.

In the interactive below, drag the steps that Carla and Crystal might use into the correct order by clicking and dragging on the tile from the "Symbolic Steps" box. Identify the property of real numbers that justifies why Carla and Crystal can do that step with the symbolic representation of the inequality by clicking and dragging on the tile from the "Properties" box. You may use some properties more than once or not at all.

Which of the following points lie in the solution set of the inequality? In other words, which of the following ordered pairs show combinations of Costa Rica Sunrise coffee beans and Colombia’s Best coffee beans that Carla and Crystal could use in order to make a blend that satisfies their criteria?

Interactive popup. Assistance may be required.

Need a hint?

Substitute the x- and y-values into the inequality and test each point to determine which points make the inequality true.

Interactive popup. Assistance may be required.

Check Your Answer

(16, 0); (6, 3); (9, 5)
7.50x + 8.75y ≤ 120 7.50(16) + 8.75(0) ≤120 120 + 0 ≤ 120 120 ≤ 120	7.50x + 8.75y ≤ 120 7.50(6) + 8.75(3) ≤120 45 + 26.25 ≤ 120 71.25 ≤ 120	7.50x + 8.75y ≤ 120 7.50(9) + 8.75(5) ≤120 67.50 + 43.75 ≤ 120 111.25 ≤ 120
The points (0, 16), (5, 12), and (9, 10) do not satisfy the inequality.
7.50x + 8.75y ≤ 120 7.50(0) + 8.75(16) ≤120 0 + 140 ≤ 120 140 120	7.50x + 8.75y ≤ 120 7.50(5) + 8.75(12) ≤120 37.50 + 105 ≤ 120 142.50 120	7.50x + 8.75y ≤ 120 7.50(9) + 8.75(10) ≤120 67.50 + 87.50 ≤ 120 155 120

Practice

Hope and Todd run a small business producing snack boxes. Almonds cost $8.25 per pound and cashews cost $12.50 per pound. They want to keep the cost of one batch of snack mix below $225. Hope wrote the inequality 8.25x + 12.50y < 225, where x represents the number of pounds of almonds, and y represents the number of pounds of cashews in a batch of snack mix.

1. Write the inequality in slope-intercept form so that Todd can use a graphing calculator’s function editor to graph the inequality.

   Interactive popup. Assistance may be required.

   Need a hint?

   Slope-intercept form of a linear relationship is y = mx + b.

   Interactive popup. Assistance may be required.

   Check Your Answer

   8.25x + 12.50y < 225 8.25x – 8.25x + 12.50y < -8.25x + 225 12.50y over 12.50 12.50y 12.50 < -8.25x over 12.50 -8.25x 12.50 + 225 over 12.50 225 12.50 y < -0.66x + 18

   

2. Which of the following combinations of almonds and cashews could Hope and Todd use to create their snack mix?

   Snack Mix
   Almonds (lb)	3	7	5	11
   Cashews (lb)	14	14	12	10

   Interactive popup. Assistance may be required.

   Need a hint?

   Let the number of pounds of almonds equal x and the number of pounds of cashews equal y. Substitute the values for x and y into the inequality and test each ordered pair.

   Interactive popup. Assistance may be required.

   Check Your Answer

   8.25x + 12.50y < 225 8.25(3) + 12.50(14) < 225 24.75 + 175 < 225 199.75 < 225	8.25x + 12.50y < 225 8.25(7) + 12.50(14) < 225 57.75 + 175 < 225 232.7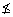5 225
   8.25x + 12.50y < 225 8.25(5) + 12.50(12) < 225 41.25 + 150 < 225 191.25 < 225	8.25x + 12.50y < 225 8.25(11) + 12.50(10) < 225 90.75 + 125 < 225 215.75 < 225
   (3, 14), (5, 12), and (11, 10) are combinations that fit within the constraint of $225 per batch of snack mix.