You may have previously investigated different ways to determine if a given ordered pair was a solution to a linear inequality.

Is (-1, -7) a solution for 4x − 2y > 8?
Use substitution.

If we substitute -1 for x and -7 for y, we will have the following:

4x − 2y > 8
4(-1) − 2(-7) > 8
-4 + 14 > 8
10 > 8

Since 10 is greater than 8, we know that (-1, -6) is a solution to the inequality.

Make a table of values.

Step 1:

Enter the inequality in the function editor (Y=).


Remember that first, you may need to write the inequality in Y = form, or solve the inequality for y.

        4x − 2y > 8
4x – 4x − 2y > -4x + 8
             -2y > -4x + 8
              -2y over -2 -2y -2 > -4x over -2 -4x -2 + 8 over -2 8 -2

                 y < 2x − 4



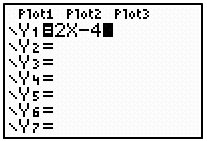
Step 2:

Look at the table of values. Scroll to locate the x-value of -1.


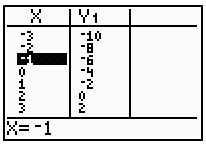
The table of values shows that when x = -1, y = -6. Our test point is (-1, -7). Compare the y-value from the table with the y-value from the test point.

y-value from test point < y-value from table -7 < -6

Since the y-value from the test point is less than the y-value from the table, the test point makes the inequality true. So, we know that (-1, -7) is a solution to the inequality.
Use a graph.

Step 1:

Enter the inequality in the function editor (Y=).


Remember that first, you may need to write the inequality in Y = form, or solve the inequality for y.

        4x − 2y > 8
4x – 4x − 2y > -4x + 8
             -2y > -4x + 8
              -2y over -2 -2y -2 > -4x over -2 -4x -2 + 8 over -2 8 -2

                 y < 2x − 4



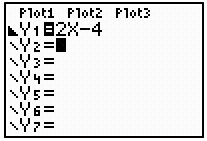
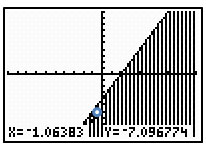
Because we want to see y-values that are less than the expression 2x – 4, set the graph to shade beneath the graph.

Step 2:

Look at the graph. Locate the test point, (-1, -7).


Because the test point lies within the shaded region, we know that (-1, -7) is a solution to the inequality.

In this lesson, you will look more closely at solving linear inequalities using two methods: graphs and properties of equality. You will also use those methods to solve linear inequalities that represent real-world situations.