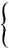
m = -3n
m = 10 – 4n
Substitution is used to check the problem.
- One variable is solved for in one of the equations. The system is solved by substituting the equation with the isolated term into the other equation:
- One variable can be easily solved. The system is solved by solving for one variable in one of the equations then substituting the equation into the second equation: (Solve for a in the second equation then substitute the second equation into the first equation.)
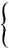
x + 2y = 7
y = x – 5
Graphing is used to check the problem.
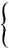
2a + 3b = 2
a – 2b = 8
Graphing or elimination is used to check the problem.
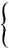
8x + 11y = 37
2x – 11y = -7
Graphing is used to check the problem.