
As you have seen in previous resources, linear equations can be written in two forms.

In addition to determining and interpreting intercepts from graphs and tables, you can also determine and interpret intercepts directly from an equation.

![]() In the interactives below, drag the steps of solving the equation into the correct order. Use the completed solutions to look for patterns in how you can determine the x-intercept and y-intercept for a linear equation that is given in slope-intercept form.
In the interactives below, drag the steps of solving the equation into the correct order. Use the completed solutions to look for patterns in how you can determine the x-intercept and y-intercept for a linear equation that is given in slope-intercept form.
How can you determine the x-intercept and y-intercept from an equation in slope-intercept form, y = mx + b?
Interactive popup. Assistance may be required. The x-intercept is the point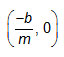 , and the y-intercept is the point (0, b).
, and the y-intercept is the point (0, b).
![]() In the interactives below, drag the steps of solving the equation into the correct order. Use the completed solutions to look for patterns in how you can determine the x-intercept and y-intercept for a linear equation that is given in standard form.
In the interactives below, drag the steps of solving the equation into the correct order. Use the completed solutions to look for patterns in how you can determine the x-intercept and y-intercept for a linear equation that is given in standard form.
How can you determine the x-intercept and y-intercept from an equation in standard form, Ax + By = C?
Interactive popup. Assistance may be required. The x-intercept is the point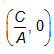 , and the y-intercept is the point
, and the y-intercept is the point 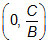 .
.
Interpret both intercepts in the relationships below.
Interactive popup. Assistance may be required.
Set each variable equal to 0 and solve for the other variable. Interactive popup. Assistance may be required.
The m-intercept, (-25.45, 0), shows that the fixed monthly charge is approximately equal to the amount of money that 25.45 minutes cost.
Interactive popup. Assistance may be required.
The m-intercept, (-25.45, 0), shows that the fixed monthly charge is approximately equal to the amount of money that 25.45 minutes cost. 
Interactive popup. Assistance may be required.
Set each variable equal to 0 and solve for the other variable. Interactive popup. Assistance may be required.
The x-intercept, (30, 0), shows that in 30 months, the remaining balance will be equal to $0, or in other words, Subkhir’s car loan will be paid in full.
Interactive popup. Assistance may be required.
The x-intercept, (30, 0), shows that in 30 months, the remaining balance will be equal to $0, or in other words, Subkhir’s car loan will be paid in full.
Interactive popup. Assistance may be required.
Set each variable equal to 0 and solve for the other variable. Interactive popup. Assistance may be required.
The x-intercept, (6, 0), shows that if Nimitha buys only oranges, she can buy 6 pounds of oranges.
Interactive popup. Assistance may be required.
The x-intercept, (6, 0), shows that if Nimitha buys only oranges, she can buy 6 pounds of oranges.