In a previous resource, you met the Williams family, who took a road trip to visit relatives for the holidays. Mrs. Williams drives at an average speed of 60 miles per hour. You used a table to represent the situation where Mrs. Williams drove for x hours and covered a distance of y miles.

Now, let’s consider the situation where the Williams family is coming home from visiting relatives. Mrs. Williams has to drive 350 miles in order to get home. Even though there is road construction, the family still drives at a constant rate; however, it takes them longer to drive home than it did to get to their relatives' house. Shonda Williams was bored, so she kept track of how many miles, y, remained until they got home after a certain amount of time, x, had passed. Shonda’s data appears in the table below.

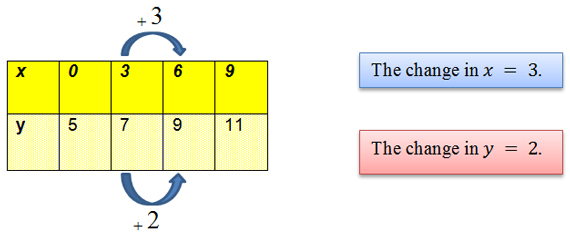
Use the interactive below to help you determine the slope of the function representing the Williams family’s return trip home.

Mouse over each row of the table to see the change in x and the change in y. Use that information to calculate the slope of the function. Remember, slope is the ratio of the change in y to the change in x.

What is the slope of the linear function representing the relationship between the amount of time since leaving the Williams family’s relatives’ house, x, and the number of miles remaining, y, until the Williams family is back home?

Remember, slope can be found using the following formula:

Check Your Answer

You can use any one of the following pairs of numbers in the table to calculate the slope.

Slope = change in y over change in x Change in y Change in x = 340 miles – 170 miles over 4 hours – 2 hours 300 miles – 325 miles 1 hour – 0.5 hours = 170 miles over 2 hours - 25 miles 0.5 hours = - 50 miles per hour

Slope = change in y over change in x Change in y Change in x = 340 miles – 170 miles over 4 hours – 2 hours 275 miles – 300 miles 1½ hours – 1 hour = 170 miles over 2 hours - 25 miles ½ hour = - 50 miles per hour

Slope = change in y over change in x Change in y Change in x = 340 miles – 170 miles over 4 hours – 2 hours 225 miles – 275 miles 2.5 hours – 1½ hours = 170 miles over 2 hours - 50 miles 1 hour = - 50 miles per hour

Slope = change in y over change in x Change in y Change in x = 340 miles – 170 miles over 4 hours – 2 hours 150 miles – 225 miles 4 hours – 2.5 hours = 170 miles over 2 hours - 75 miles 1.5 hours = - 50 miles per hour

Pause and Reflect

If you select a different pair of numbers from the table, do you get a different value for the slope? Why do you think that is the case?

Check Your Answer

No. Linear functions have a constant slope, or constant rate of change, so it will not matter which pair of corresponding values that you select from the table, you will always get the same slope.

How is this method related to the slope formula?

Check Your Answer

The slope formula, m = y₂ – y₁ x₂ – x₁ , also uses the ratio of the change in y to the change in x. If you select two points from the table, you can also use the slope formula to determine the slope of the line represented by the ordered pairs in the table.

Practice

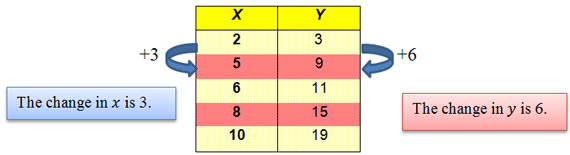
Using the tables below, find the change in y and x to determine the slope.

1. X	Y
   2	3
   5	9
   6	11
   8	15
   10	19

   
   Interactive popup. Assistance may be required.

   Check Your Answer

   The slope is 2. slope = six over three 6 3 = 2.
   

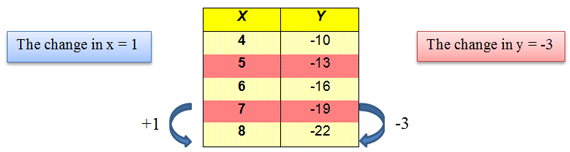
2. X	Y
   4	-10
   5	-13
   6	-16
   7	-19
   8	-22

   
   Interactive popup. Assistance may be required.

   Check Your Answer

   The slope is -3. slope = negative three over one -3 1 = -3.
   

3. X	0	3	6	9
   Y	5	7	9	11

   
   Interactive popup. Assistance may be required.

   Check Your Answer

   Slope = two over three 2 3 .