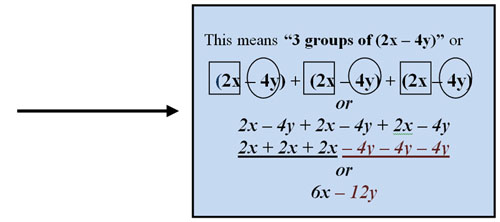
Another way to write this with
the Distributive Property would be
3(2x - 4y) 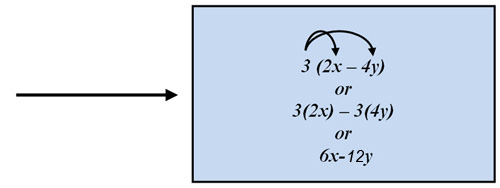
Sometimes before we add or subtract to simplify the polynomial, we have to multiply. When this happens we use the distributive property.
Let's look at an example of simplifying with and without the distributive property.
Example 1. 3(2x - 4y)
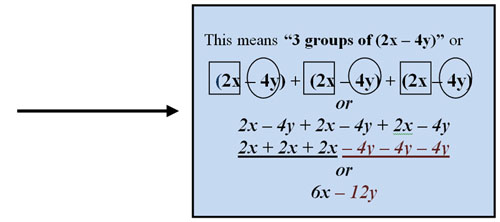 |
|
Another way to write this with |
Which way was simpler to use?
Using what you have learned so far, simplify each of the following polynomials by combining like terms. Click the link below each problem to check your work.
1. 3x – 4y – 2x + 8y + 5x
Interactive popup. Assistance may be required.
6x + 4y
2. 4(2x – 9y)
Interactive popup. Assistance may be required.
8x - 36y
3. 2(5a – 3b + 4c)
Interactive popup. Assistance may be required.
10a - 6b + 8c
4. x2 – 4x – 6 + 5x2 + 3x4 – 7x2
Interactive popup. Assistance may be required.
3x4 - x2 - 4x - 6
Hey, this is not so bad!