I don't know how many brick walls you've constructed in your day, but to increase stability, a brick layer will alternate each row by starting the row of bricks with half a brick. Below is a drawing of a triangular wall six rows high.

a triangular brick wall 6 bricks high is shown

Question: What expression would describe how many bricks a brick layer would need to build a triangular wall n rows high?

Follow the steps below to help solve this problem.

  1. Create a table
  2. Draw a graph
  3. Write an expression
  4. Check

Create a Table

Think about how you would label this table. What would your column headers be? Click on the lines in the table to reveal the column headers.

____ ____
   
   
   
   
   
   

Now we can fill in the table. It will be easier if we break down the picture. Determine how many bricks are in each drawing. Scroll down to see the table.

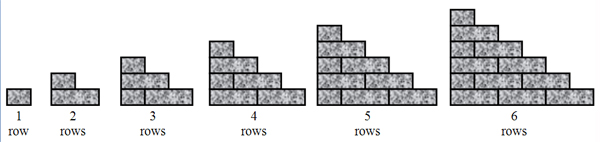
The triangular brick wall has been broken down to individual rows. Row 1 is a half-brick. Row 2 is 1 brick. Row 3 is 1 ½ bricks, etc.

Explanation

You may argue that in a 1-row wall you used a whole brick. You used half a brick and threw the other half away. No, you're saving it for another wall. The same thing applies for a 2-row and a 5-row wall. You are saving the extra half brick for another wall.
Rows, n Number of Bricks
1 0.5
2 1.5
3 3
4 5
5 7.5
6 10.5

Great! We have a table.

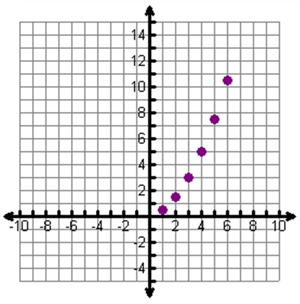
Next, Graph. Let's plot these points. Think about how you would set up a graph of this data.

Scroll down to see the graph.

A graph of the data in the table is shown
Rows, n Number of Bricks
1 0.5
2 1.5
3 3
4 5
5 7.5
6 10.5

That doesn't look like a line.

At this point you may or may not be able to come up with the expression on your own. Suppose this question were given to you as multiple choice.

Use your graphing calculator and what you learned in Sections 1 and 2 of this resource to answer the question: Which expression would describe how many bricks a brick layer would need to build a triangular wall n rows high?

The triangular brick wall has been broken down to individual rows. Row 1 is a half-brick. Row 2 is 1 brick. Row 3 is 1 ½ bricks, etc.
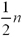
  1. 1/2 to the nth power
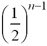
  2. one-half to the (n minus 1) power
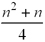
  3. (n-squared plus n) divided by 4
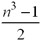
  4. (n-cubed minus 1) divided by 2

Use your notes to record your answer explaining how you know your answer is correct.