If you did not get to make the Spaghetti Bridge, you can still work with data that someone else has collected. This table shows the data collected by someone else for a Spaghetti Bridge.

You may want to make predictions such as how many marbles a 10 spaghetti bridge could hold.

Go to this interactive webpage and input your data into the box below the graph.

Regression Activity

1. Remember to put a comma between the pieces of spaghetti and the number of marbles.
2. After each pair of numbers, press enter.
3. Then press Update Plot.
4. When your points are plotted, you can check the box labeled Display the line of best fit to see the line graphed and the equation for the line of best fit.

This line of best fit is the closest line that can approximate the data from the Spaghetti Bridge. This equation can now be used to estimate how many marbles 10 pieces of spaghetti would hold. Your activity page should now look something like the following image.

Source: http://www.shodor.org/interactivate/

To estimate the number of marbles, you can substitute 10 in for the pieces of spaghetti, x-value, or you can reset the graph by pressing Set Window window.

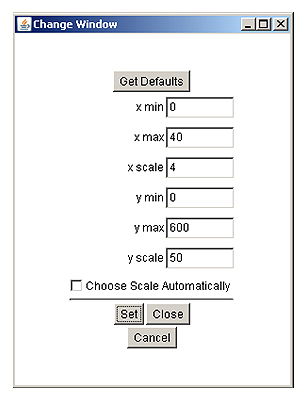
The Change Window will open (as shown on the right) to set the x and y values for the graph. Since you know you want to see at least 10, set the x-value for 12 and set the y-value for a higher number.  Press Set at the bottom to change the window and then press Close to see your graph. Can you see the value for 10? If not, set the window again to a larger y-value.

Answer the following questions using your notes.

1. What was the estimate of how many marbles 10 pieces of spaghetti would hold?
2. Was the estimate larger than you thought?
3. Why do you think the number was so large?
4. Did the graph give you a clue that the number was going to be large?
5. Does this line of best fit show a positive correlation, a negative correlation or no correlation?