The last part of this resource is writing equations for quadratic functions. This is the form of a quadratic function.

y = ax² + bx + c

Quadratic functions are parabolas and either have a bowl shape or a mountain shape. Parabolas with a positive a value have a bowl shape and those with a negative a value have a mountain shape.

In addition, you know how to use a calculator to check for the correct answer so you can input these equations in the equation editor (Y=) as well.

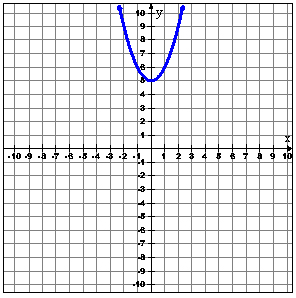
Which quadratic equation best represents the parabola shown below?

y = x2 + x + 5 y = x2 + 5 y = -x2 + 5 y = -x2 + x + 5

Test each of the answer choices to eliminate obviously wrong answers. C and D are obviously wrong.

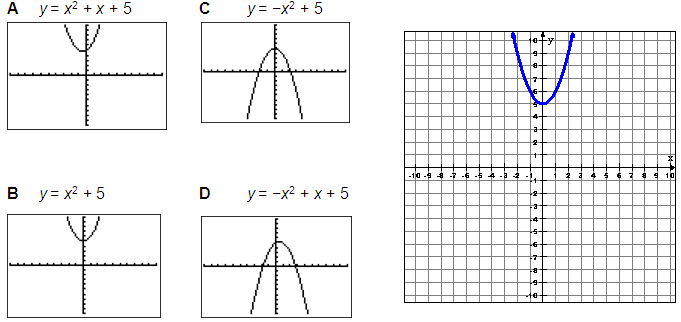
We’ve eliminated C and D.

The graph you were given contains the points (-2, 9), (-1, 6), (0, 5), (1, 6), and (2, 9). Use the TABLE.

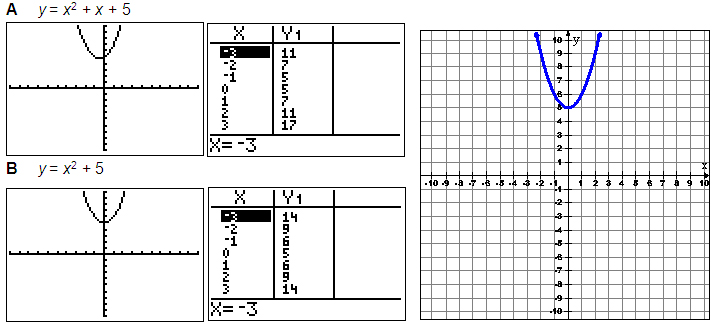
Now you can confidently pick choice B as your answer.

Remember, you can also use the TRACE key to check points on the graph. Press TRACE, type in the x-value, and press ENTER.

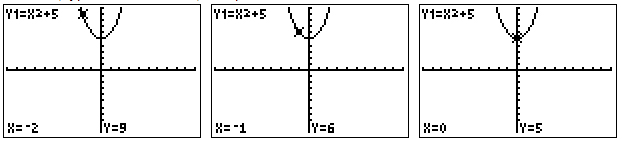
Write the answer to this question using your notes.

The graph of y = -x² + 5 and y = -x² + x + 5 open downward. Describe how you know the graph will open downward strictly from the equation.

Check Your Answer

The equation has a negative x² term.

Now solve this problem.

Which quadratic equation best represents the parabola shown below?

Interactive popup. Assistance may be required. y = x2 - 4 y = x2 − 4 Incorrect, this graph would NOT contain (1,−2). Interactive popup. Assistance may be required. y = -4x2 y = −4x2 Incorrect, this parabola would open down. Interactive popup. Assistance may be required. y = x2 + x − 6 y = x2 + x – 6 Incorrect, the graph would NOT contain (1,−2). Interactive popup. Assistance may be required. y = x2 + x − 4 y = x2 + x – 4 Correct!  Did you check points?