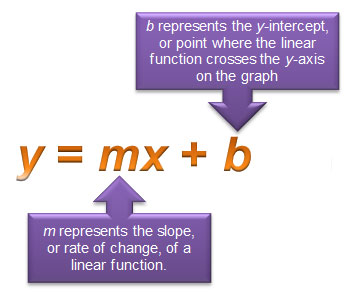
You may have studied ways to represent a linear function using the starting point and a rate of change. You may have called this form of a linear function slope-intercept form.

Use what you know about slope-intercept form of linear equations to build inequalities from each of the following situations.

Pause and Reflect

How is building an inequality in slope-intercept form similar to building an equation in slope-intercept form? How is it different?

Interactive popup. Assistance may be required.

Click here to see a possible answer.

For both equations and inequalities in slope-intercept form, there is an initial amount and a number of items that is multiplied by the rate of change. For equations, the sum (of the initial amount and product of the rate of change and amount of items) is equal to a given number. For inequalities, the sum is compared to an upper limit (for “less than” conditions) or a lower limit (for "greater than" conditions).

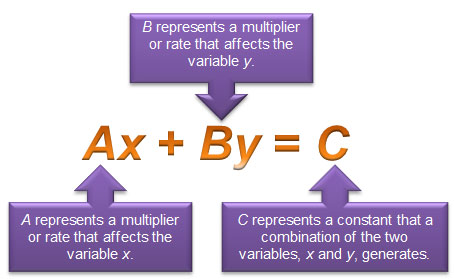
You also examined situations that could result in equations written in standard form. Standard form of a linear equation is Ax + By = C. In this representation, A, B, and C are constants that show the relationship between two variables, x and y.

Pause and Reflect

When writing the inequalities in standard form, how did you determine the coefficients for each of the variables?

Interactive popup. Assistance may be required.

Check Your Answer

A rate, or multiplier, that relates to the number of items described by a variable becomes the coefficient for that variable.

Practice

1. Ms. Gleason is opening a new restaurant. She has enough booths to seat up to 40 people. She is ordering tables to fill the rest of the seating space. Each table can seat up to 6 people, and she plans to seat up to 125 people in the dining area. Write an inequality that Ms. Gleason can use to determine the number of tables, t, that she needs to order.
   

   Interactive popup. Assistance may be required.

   Need a hint?

   Does 125 represent an upper limit (< or ≤) or a lower limit (> or ≥)?
   Interactive popup. Assistance may be required.

   Check Your Answer

   40 + 6t ≤ 125
2. Teachers at Harris High School are not allowed to make more than 2,000 copies per month. Mrs. Sheppard has already made 750 copies this month, and has 120 students. Write an inequality showing the number of activity sheets, s, that Mrs. Sheppard may copy this month so that each of her students will have one copy.

   Interactive popup. Assistance may be required.

   Need a hint?

   Does 2,000 represent an upper limit (< or ≤) or a lower limit (> or ≥)?
   Interactive popup. Assistance may be required.

   Check Your Answer

   750 + 120s ≤ 2,000
3. Michael is raising money for his football league. Chocolate bars sell for $2.50 each and chocolate mints sell for $3.50 each. If Michael wants to raise more than $150, write an inequality showing the number of chocolate bars, b, and the number of chocolate mints, m, he must sell.

   Interactive popup. Assistance may be required.

   Need a hint?

   Does $150 represent an upper limit (< or ≤) or a lower limit (> or ≥)?
   Interactive popup. Assistance may be required.

   Check Your Answer

   2.50b + 3.50m > 150