A linear function is a function with a constant rate of change. In a linear function, the x-values change by a constant amount and the y-values change by a constant amount.
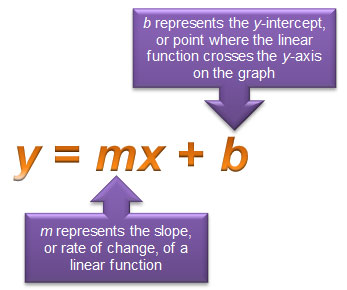
One way that you can represent a linear function is called slope-intercept form.

When you have a situation with a starting point, or initial condition, and a constant rate of change, you can frequently represent that situation using a linear function in slope-intercept form.
You may also see situations that result in equations written in standard form. Standard form of a linear equation is Ax + By = C. In this representation, A, B, and C are constants that show the relationship between two variables, x and y.
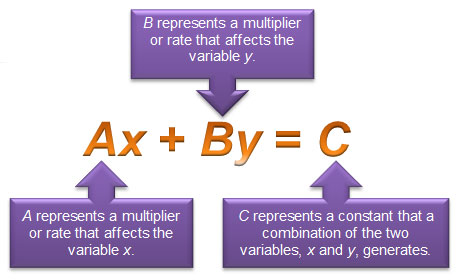
![]() Now, you are going to practice writing equations when given a verbal description. Drag the matching equation under the appropriate label. When you have completed the matching, copy or print the page into your notebook.
Now, you are going to practice writing equations when given a verbal description. Drag the matching equation under the appropriate label. When you have completed the matching, copy or print the page into your notebook.
When writing the equations in slope-intercept form, how did you determine the coefficient for the variable?
Interactive popup. Assistance may be required. The coefficient is the rate of change presented in the situation.
When writing the equations in slope-intercept form, how did you determine the addend, or the value of b?
Interactive popup. Assistance may be required. The addend, or the value of b, is the starting point, or initial value, in the situation.
When writing the equations in standard form, how did you determine the coefficients for each of the variables?
Interactive popup. Assistance may be required. A rate, or multiplier, that relates to the number of items described by a variable becomes the coefficient for that variable.
Interactive popup. Assistance may be required.
Which rate depends on the number of people, and which fee is the same regardless of the number of people? Interactive popup. Assistance may be required.
c = 10 + 7p
Interactive popup. Assistance may be required.
c = 10 + 7p 

Interactive popup. Assistance may be required.
Which rate depends on the number of miles, and which fee is the same regardless of the number of miles? Interactive popup. Assistance may be required.
26 = 3.6 + 1.6m
Interactive popup. Assistance may be required.
26 = 3.6 + 1.6m 
Interactive popup. Assistance may be required.
When you are taking a discounted price, what operations do you need to consider? Interactive popup. Assistance may be required.
s = r – 0.2r OR s = 0.8r
Interactive popup. Assistance may be required.
s = r – 0.2r OR s = 0.8r 

Interactive popup. Assistance may be required.
Which rate depends on the number of months, and which amount is the same regardless of the number of months? Interactive popup. Assistance may be required.
a = 350 + 50m
Interactive popup. Assistance may be required.
a = 350 + 50m 
Interactive popup. Assistance may be required.
Use the cost per pound as a multiplier for each variable. Interactive popup. Assistance may be required.
12.50c + 9.25e = 32
Interactive popup. Assistance may be required.
12.50c + 9.25e = 32 