Pedro adds a 75% acid solution to 10 milliliters of solution that is 15% acid. The function that represents the percent of acid in the resulting solution is f(x) = 10(0.15) + x(0.75) 10 + x , where x is the amount of 75% solution added.

Use the equation to solve the following:

  1. If Pedro adds 30 ml of the 75% solution, what percent of acid is the resulting solution?
    2. Interactive popup. Assistance may be required.

    Check Your Answer

    60% Close Pop Up

    We have three methods that can be used to find the answer to this question.

    We can substitute 30 ml in for x and use algebra/arithmetic to simplify: f(x) = 10(.15) + 30(.75)m 10 + 36 = 24 40 = .6
    The resulting solution is 60% acid.

    We can enter the function into the graphing calculator and use either the graph or the table to find the answer.

    Remember that parentheses are needed to tell the calculator to group the numerator and to group the denominator:

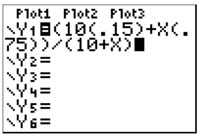
    If graphing, adjust the window, use the trace button and type in the x-value you are looking for, and enter.

    If using the table, set the table to start at the x-value you are looking for, and select table.

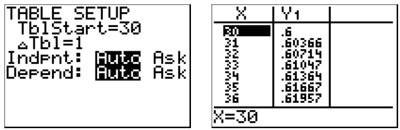
    All three methods show that adding 30 ml of the 75% acid solution to the 10 ml of the 15% acid solution would result in 40 ml of a 60% acid solution.

  2. How much 75% solution should be added to create a solution that is 36% acid?
    3. Interactive popup. Assistance may be required.

    Check Your Answer

    5.4ml Close Pop Up

    Let's look at those three methods to find this answer.

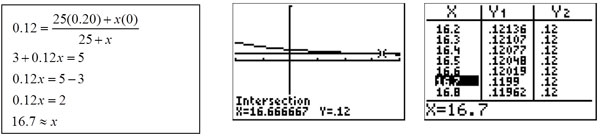
    Algebraically, we need to substitute 36 into the function rule for y. Then, we need to solve the equation for x.

    0.36 = 10(0.15) + x(0.75) 10 + x
    3.6 + 0.36x = 1.5 + 0.75x
    3.6 - 1.5 = 0.75x - 0.36x
    2.1 = 0.39x
    5.4 ≈ x

    If using the graphing method, because you have a y-value instead of an x-value, you want to enter 36% in decimal form into y2. The graph needs to show the point of intersection. Use the calculate feature of the calculator, select the intersect feature, and enter until you see the point of intersection indicated in the calculator window.

    If using the table feature, it is not necessary but could be helpful, to enter the 36% in decimal form into Y2.You will need to scroll through the table until you find 0.36 in the Y1 column. This value is not visible in the standard table, but you can see that 0.36 comes between 0.35 and 0.375 so the answer is between 5 and 6. Start the table at 5 and go by tenths instead of ones to get a more accurate answer.

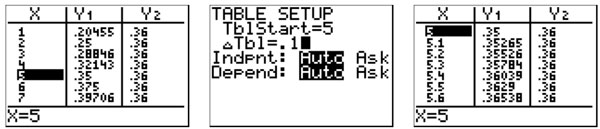
    All three methods give us an answer of approximately 5.4. Pedro should add about 5.4 ml of the 75% acid solution to the 10 ml of the 15% acid solution to get a solution that is 36% acid.

  3. What if Pedro has 18 ml of a 25% solution and he is going to add pure acid? Adapt his function to the new situation and then find the amount of pure acid he needs to add so that a resulting solution is 46% acid.
    4. Interactive popup. Assistance may be required.

    Check Your Answer

    Adapting his function to the new situation is a review of Module 7 Lesson 5.

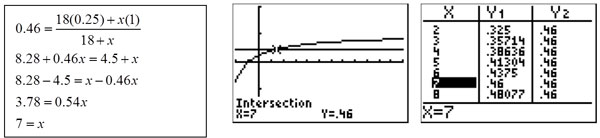
    We'll replace 10 ml in the old equation with 18 ml, replace 0.15 with 0.25, replace 0.75 with 1 (pure acid is 100% acid and as a decimal 100% is 1). The new function is f(x) = 18(0.25) + x(1) 18 + x

    The three methods for finding the amount of pure acid to be added follow.

    Close Pop Up
  4. Anita is working with Pedro. She has 25 ml of a 20% acid solution. How much water should she add to dilute the solution to 12% acid? Show how Anita adapted Pedro's function to get the answer to her situation.
    5. Interactive popup. Assistance may be required.

    Check your answer

    For Anita's equation we'll replace 10 ml in the old equation with 25 ml, replace .15 with .20, replace .75 with 0 (water is 0% acid). The new function is f(x) = 25(0.20) + x(0) 25 + x .

    The three methods for finding the amount of pure acid to be added follow.

    Close Pop Up