The solution of any inequality is based on the domain of the function. Domains of functions are usually restricted when there is a variable in the denominator of a fraction or when there is a radical that has an even index (ex. √x or ∜x).
Find the domain of the square root parent function y = √x.
x ≥ 0 because you can only use x-values that are positive or equal to 0. The square root of a negative number is imaginary and not considered part of the domain.
The solution of an equation or inequality must be part of the domain.
Once the domain is found, the range and which quadrant(s) the graph lies in are found.
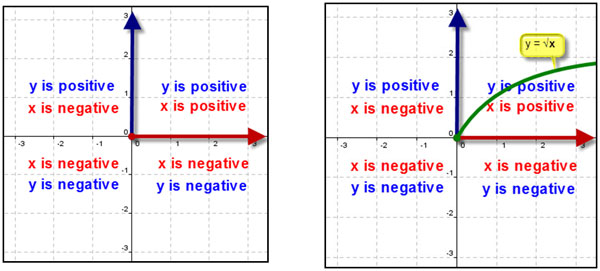
Find the range and in which quadrant(s) the square root parent function y = √x graph lies. Justify your answer.
y ≥ 0 because the function is + √x, the square root values will only be positive or equal to 0.
x-values are positive only in the 1st or 4th quadrants
y-values are positive only in the 1st and 2nd quadrants
The graph lies in the quadrant(s) that the domain and range have in common—1stquadrant

Because of a restricted domain, there may be a part of the coordinate plane that does not contain possible solutions.
The equation y =, can be written as different inequalities each one using one of the four inequality symbols <, ≤, >, or ≥ .
Note: Inequalities have one, an infinite (Hyperlink to the term in the glossary) number, or no solutions.