Example:
3x2 = 5x + 2
3x2 – 5x = 2
3x2 – 5x 3 numerator: 3x squared − 5x, denominator: 3 = 2 3 two-thirds
x2 – 5 3 five-thirds x = 2 3 two-thirds
x2 – 5 3 five-thirds x + 25 36 numerator: 25, denominator: 36 = 2 3 two-thirds + 25 36 k numerator: 25, denominator: 36
=
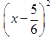49
36
numerator: 49, denominator: 36
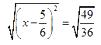
x – 5 6 five-sixths = ± 7 6 seven-sixths
x – 5 6 five-sixths = 7 6 seven-sixths or
x = 12 6 twelve-sixths
x = 2
x – 5 6 five-sixths = - 7 6 seven-sixths
x = – 2 6 two-sixths
x = - 1 3 one-third
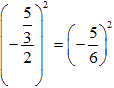Move the linear term to the left side of the equation.
Divide both sides of the equation by 3.
Simplify, and leave in rational form.
b =
-5 over 3
5
3
and 
=
25 over 26
25
26
. Add
25 over 26
25
26
to both sides of the equation.
Write the left side of the equation in factored form and simplify the right side of the equation.
Take the square root of both sides.
Solve for x.
The solutions are 2 and - 1 3 one-third
Use your own paper to fill in the blanks.
x2 + 14x + 49 = 100
(x + ___)2 = 100
x + ___ = ± ___
x = ___ or x = ___
x2 + 14x + 49 = 100
(x + 7)2 = 100
x + 7 = ± 10
x = 3 or x = -17
3x2 – 36x + 33 = 0
3x2 – 36x = ___
3x2 – 36x ? numerator: 3x squared − 36x, denominator: blank = ? ? fraction: blank over blank
x2 – ___x = -11
x2 – 12x + ___ = -11 + ___
(x – ___)2 = 25
x – 6 = ± ___
x = ___ or x = ___