What happens if we change "a" in y = a | x - h | + k ?

The parameter “a” has two possible effects on the graph:

1. If “a” is positive (a > 0), the absolute value graph opens up.
   If “a” is negative (a < 0), the absolute value graph reflects across the x-axis and opens down.
   reflection - is a transformation that happens when a graph "flips" across a line (called the line of reflection), only the location of the graph changes; the shape stays the same

   Close
2. If | a | > 1, then the absolute value graph is narrower than the graph of the parent function.
   (The graph has been stretched.)
   
   stretch – a transformation that pulls the points of a graph vertically away from the x-axis, stretching an absolute value graph makes it narrower

   Close
   If 0 < | a | < 1, then the absolute value graph is wider than the graph of the parent function.
   (The graph has been compressed.
   • We use the absolute value of “a” because the sign of “a” does NOT affect the openness of the absolute value graph.
   • The sign of “a” ONLY determines whether the absolute value graph opens up or down.

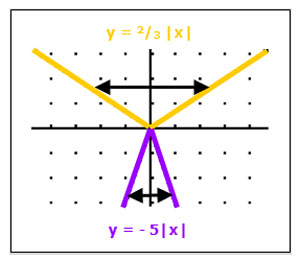
Example: Determine which of the functions is the widest: y = -3 | x | or y = two-thirds 2 3 | x |

The coefficient of | x | “a”, determines:

• whether the absolute value graph opens up or down and
• the openness of the absolute value graph

• Remember that the sign of “a” ONLY determines whether the absolute value graph opens up or down. The openness of the absolute value graph is determined by | a |.

| two-thirds 2 3 | = two-thirds 2 3 and | -5 | = 5

Since two-thirds 2 3 < 5, then y = two-thirds 2 3 | x | is wider than y = -5 | x |.

Close this window or tab to return to the lesson.