
Problem 1
Solve the system using elimination: During one cold football game, the math club made $685 selling large cups of hot chocolate and coffee. They used 420 cups and sold the hot chocolate for $1.75 per cup and the coffee for $1.25 per cup. Write a system of equations that could be used to determine how many cups of each type of drink they sold.
Solution:
Let h = the number of cups of hot chocolate they sold
Let c = the number of cups of coffee they sold
The system modeling this situation is:
h + c = 420
1.75h + 1.25c = 685
Use elimination to now solve the system.

The system needs to be prepared for elimination because just adding the two equations right now would not eliminate a variable. You first want to look through the equation to see if any of the coefficients for the variables is 1. Both variables in the first equation have a coefficient of 1, so you can eliminate either one.
If you choose to eliminate h, you will need to multiply the first equation by -1.75, which is the opposite of the coefficient of h in the second equation. If you choose to eliminate c, you will need to multiply the first equation by -1.25 which is the opposite of the coefficient of c in the second equation. This solution will eliminate c.
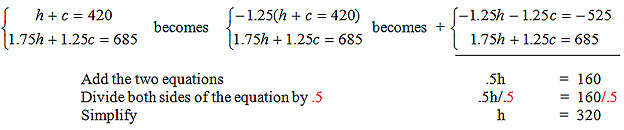
Find the value of c by substituting 320 in for h in one of the original equations
I chose the first equation because it does not have decimals.
h + c = (320) + c = 320 – 320 + c = c = |
420 420 420 – 320 100 |
first equation Replace h with 320 Subtract 320 from both sides of the equation Simplify |
Check the accuracy of your point by substituting in both 320 and 100 into the second equation—the equation that we did not use to find c.
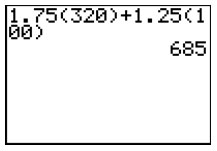
Since 685 is what we were supposed to get, we did the work correctly.
The Math Club sold 320 cups of hot chocolate and 100 cups of coffee.

Problem 2
Mrs. Jimenez, the drama teacher at North High, bought 16 student tickets and 2 adult tickets to the play Wicked and paid $676. Her counterpart, Mr Ashraf, at South High, bought 28 student tickets and 3 adult tickets and paid $1154.
Define variables, set up a system of equations, and solve that system using elimination to find the cost of each student and each adult ticket.
Let s = the cost of a student ticket in dollars
Let a = the cost of an adult ticket in dollars
Mrs. Jimenez's purchase 16s + 2a = 676
Mr. Ashraf's purchase 28s + 3a = 1154

The system needs to be prepared for elimination because just adding the two equations right now would not eliminate a variable. Looking through the equations, we see that none of the coefficients for the variables is 1.
Now, it is time to look for a least common multiple. Remember how you had to think when you were looking for a common denominator when you added or subtracted fractions? Well, that is how you think now, just without the fractions

If we choose to eliminate s, we must get both coefficients to be 112, one positive & one negative, because 112 is the smallest number that both 16 and 28 go into evenly.
If we choose to eliminate a, we must get both coefficients to be 6, one positive & one negative, because 6 is the smallest number that both 2 and 3 go into evenly. Since 6 is much smaller than 112, we are going to eliminate a.

Let s = the cost of a student ticket in dollars
Let a = the cost of an adult ticket in dollars
Mrs. Jimenez's purchase 16s + 2a = 676
Mr. Ashraf's purchase 28s + 3a = 1154
The system needs to be prepared for elimination because just adding the two equations right now would not eliminate a variable. Looking through the equations, we see that none of the coefficients for the variables is 1.
Now, it is time to look for a least common multiple. Remember how you had to think when you were looking for a common denominator when you added or subtracted fractions? Well, that is how you think now, just without the fractions.
If we choose to eliminate s, we must get both coefficients to be 112, one positive and one negative, because 112 is the smallest number that both 16 and 28 go into evenly.
If we choose to eliminate a, we must get both coefficients to be 6, one positive and one negative, because 6 is the smallest number that both 2 and 3 go into evenly. Since 6 is much smaller than 112, we are going to eliminate a.
We will need to multiply the first equation by 3 so that we turn the 2a into 6a. We will need to multiply the second equation by -2 so that we turn the 3a into 6a.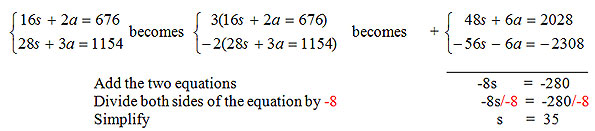
Find the value of a by substituting 35 in for s in one of the original equations
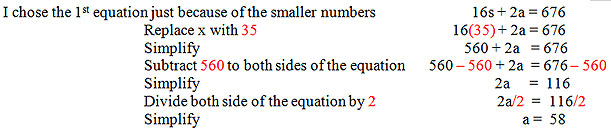
Check the accuracy of your point by substituting in both 35 and 58 into the 2nd equation—the equation that we did not use to find a.

