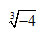
What is the value of x in the equation log _{1 2} 8 = x?

A. 64
Incorrect.

B. 2√2
Incorrect.

C. 16
Incorrect.

D. -3
Correct!

What is the value of x in the equation log _{1 3} x = -4?

A. 81
Correct! Change the equation from log form to exponential form then solve for x.

B.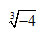

C. -4 3
Incorrect. Change the equation from log form to exponential form then solve for x.

D. -12
Incorrect. Change the equation from log form to exponential form then solve for x.

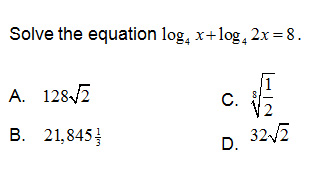
A
Correct! Change the equation from log form to exponential form then solve for x and eliminate the extraneous solution.

B
Incorrect. Simplify the left side of the equation using log rules, rewrite the equation in exponential form, solve for x and eliminate the extraneous value.

C
Incorrect. Simplify the left side of the equation using log rules, rewrite the equation in exponential form, solve for x and eliminate the extraneous value.

D
Incorrect. Simplify the left side of the equation using log rules, rewrite the equation in exponential form, solve for x and eliminate the extraneous value.

What is the domain of the equation (log)₈(x) − (log)₈(14 − 2x) = (log)₈(3x − 12)?

A. x > 7
Incorrect. Find the positive domain by evaluating each term.

B. 0 < x < 7
Incorrect. Find the domain by setting each term greater to zero.

C. 4 < x < 7
Correct! The limited domain was found, 4.

D. x < 4 or x > 7
Incorrect. Find the domain by setting each term greater to zero.

A. x = -4.449 or x = 0.449
Incorrect. Find the positive domain first, 0.

B. x = 1.646
Incorrect. Find the positive domain, use log rules, solve for x and eliminate the extraneous solution.

C. x = 1.646 or x = -3.646
Incorrect. Find the positive domain, use log rules, solve for x and eliminate the extraneous solution.

D. x = 0.449
Correct! The extraneous solutions were eliminated after finding the positive domain and using log rules to solve for x.