A new website tracked the number of visits to the site. They found that the visits grew exponentially and could be represented by the function N = 2005 · 1.26 t-1 where N represents the number of visits and t represents the number of days. To find when the number of visits will reach 250,000, solve the equation 250,000 = 2005 · 1.26 t-1.
A. t = 15
Incorrect. What is the value of t, when the value of the function is 250,000?
B. t = 22
Correct! You substituted the numbers in the equations correctly.
C. t = 32
Incorrect. What is the value of t, when the value of the function is 250,000?
D. t = 42
Incorrect. What is the value of t, when the value of the function is 250,000?
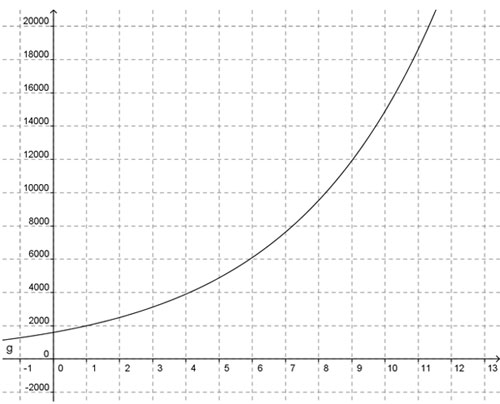
The graph below represents the function y = 2000 · 1.25x-1.

Based on this graph, which of the following is the solution to the equation 12,000 = 2000 · 1.25x-1?
A. x = 0
Incorrect. What is the value of x, when the value of the function is 12,000?
B. x = 1600
Incorrect. What is the value of x, when the value of the function is 12,000?
C. x = 2115
Incorrect. What is the value of x, when the value of the function is 12,000?
D. x = 9
Correct! If you drew in a horizontal line at y = 12,000, the horizontal line would intersect the graph at x = 9.
The table below represents the function y = 5 · 3x-2
| x | y |
| -2 | 5 81 |
| -1 | 5 27 |
| 0 | 5 9 |
| 1 | 5 3 |
| 2 | 5 |
| 3 | 15 |
| 4 | 45 |
| 5 | 135 |
| 6 | 405 |
Based on this table, which of the following is the solution for the equation 5 = 5 · 3x-2?
A. x = 2
Correct! You read the table correctly.
B. x = 135
Incorrect. What is the value of x, when the value of the function is 5?
C. x = -2
Incorrect. What is the value of x, when the value of the function is 5?
D. x = 5
Incorrect. What is the value of x, when the value of the function is 5?
Which of the following is the solution for the equation 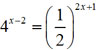 ?
?
A. x = 0.143
Incorrect. Is this the x value?
B. x = 0.81
Incorrect. If you used the calculator did you remember to use parenthesis for the entire exponent.
C. x = 0.75
Correct! Your method of solving worked.
D. No solution
Incorrect. Try using the graphing method and look for the intersection point.