State the domain, range, and vertical asymptote for the logarithmic function:
f(x) = log10(x - 2) + 3.
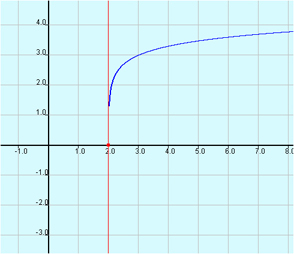
A. Domain: (-∞,∞)
Range: (1.3,∞)
Vertical Asymptote: x = 2
Incorrect. Although the picture does not show it, exponential graphs of the form f(x) = log(x + c) + d will always have an infinite range and restricted domain.
B. Domain: (2,∞)
Range: (1.3,∞)
Vertical Asymptote: x = 2
Incorrect. Although the function appears to stop close to the y-value of 1.3, it actually continues downward toward negative infinity as it gets close to the vertical asymptote.
C. Domain: (2,∞)
Range: (-∞,∞)
Vertical Asymptote: x = 2
Correct! You recognize the graph keeps moving downward as it approaches the vertical asymptote even though it appears to stop.
D. Domain: (2,∞)
Range: (-∞,∞)
Vertical Asymptote: none
Incorrect. The function has a vertical asymptote drawn in red.
State the domain, range, and vertical asymptote for the given logarithmic graph.
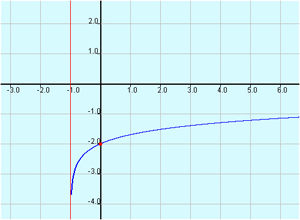
A. Domain: (1, ∞)
Range: (-∞,∞)
Vertical Asymptote: x = 1
Incorrect. The left edge of your domain and vertical asymptote are on the left (negative) side of the y-axis.
B. Domain: (-1, ∞)
Range: (-∞,∞)
Vertical Asymptote: x = -1
Correct! You identified x = -1 as an important value in finding the domain and vertical asymptote.
C. Domain: (-1, ∞)
Range: (-2,∞)
Vertical Asymptote: x = -1
Incorrect. The vertical shift of -2 units does not affect your range in any way.
D. Domain: (-1, ∞)
Range: (-∞,∞)
Vertical Asymptote: x = 1
Incorrect. Your vertical asymptote does not match the left edge of your domain.
Given f(x) = log5(x + 6) − 4, state the domain, range, and vertical asymptote for f(x).
A. Domain: (-6, ∞)
Range: (-∞,∞)
Vertical Asymptote: x = 6
Incorrect. Your vertical asymptote does not match the left edge of your domain.
B. Domain: (-6, ∞)
Range: (-4,∞)
Vertical Asymptote: x = -6
Incorrect. The vertical shift does not alter your range.
C. Domain: (-6, ∞)
Range: (-∞,∞)
Vertical Asymptote: x = -6
Correct! You found the left edge of your domain and vertical asymptote even though no graph was given.
D. Domain: (6, ∞)
Range: (-∞,∞)
Vertical Asymptote:
x = 6
Incorrect. You found the wrong horizontal shift. The expression (
x + 6) does not shift the parent function to the right 6 units.
A particular logarithmic function has a domain of (4,∞), range (-∞,∞), and vertical asymptote at x = 4. Select the equation that could represent this function.
A. f(x) = log4(x + 4) + 4
Incorrect. The (x + 4) causes a horizontal shift of 4 units to the left.
B. f(x) = log4(x + 4) − 4
Incorrect. The (x + 4) causes a horizontal shift of 4 units to the left.
C. f(x) = log4(x) + 4
Incorrect. This function has a domain of (0, ∞). It needs to shift 4 units to the right to have the proper stated domain.
D. f(x) = log2(x − 4)
Correct! You found the equation that shifted the parent logarithmic function 4 units to the right.
A. I only
Incorrect. The (x − c) shifts your function to the right c units. Check your domain again. Also, another statement (II or III) is true.
B. III only
Correct! You also recognized the correct domain is (c, ∞) and range is (-∞, ∞).
C. I and III only
Incorrect. The (x − c) shifts your function to the right c units. Check your domain again.
D. II and III only
Incorrect. The range for basic logarithmic functions of the form f(x) = a * logB(x + c) + d is not affected by the a, c, or d constants.
You are given the following facts: c and d are non-zero constants, and f(x) = 3 log10(x − c) + d. Which of these statements must be true?
I) f(x) has a domain of (-c,∞)
II) f(x) has a range of (c,∞)
III) f(x) has a vertical asymptote at x = c
A. I only
Incorrect. The (x − c) shifts your function to the right c units. Check your domain again. Also, another statement (II or III) is true.
B. III only
Correct! You also recognized the correct domain is (c, ∞) and range is (-∞, ∞).
C. I and III only
Incorrect. The (x − c) shifts your function to the right c units. Check your domain again.
D. II and III only
Incorrect. The range for basic logarithmic functions of the form f(x) = a * logB(x + c) + d is not affected by the a, c, or d constants.


